某初级中学共有学生2 000名,各年级男、女生人数如下表:
(1)已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.求x的值;
(2)现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?
(3)已知y≥245,z≥245,求初三年级中女生比男生多的概率.
A.选修4 - 1:几何证明选讲
如图,在四边形
中,
.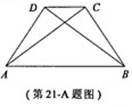
求证:
.
B.选修4 - 2:矩阵与变换
求矩阵
的逆矩阵.
C.选修4 - 4:坐标系与参数方程
已知曲线
的参数方程为
(
为参数,
),求曲线
的普通方程.
D.选修4 - 5:不等式选讲
设
,求证:
.
已知函数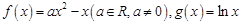 .
.
(Ⅰ)当 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性;
(Ⅱ)若函数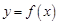 与
与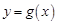 的图象有两个不同的交点
的图象有两个不同的交点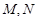 ,求
,求 的取值范围;
的取值范围;
(Ⅲ)设点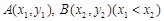 是函数
是函数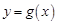 图象上的两点,平行于
图象上的两点,平行于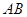 的切线以
的切线以 为切点,求证:
为切点,求证: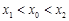 .
.
已知动圆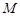 过定点
过定点 ,且和定直线
,且和定直线 相切.
相切.
(Ⅰ)求动圆圆心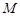 的轨迹
的轨迹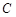 的方程;
的方程;
(Ⅱ)已知点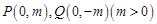 ,过点
,过点 作直线与曲线
作直线与曲线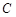 交于
交于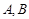 两点,若
两点,若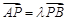 (
(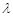 为实数),证明:
为实数),证明: .
.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,已知AB=a,AC=2,
AA1=1,点D在棱B1C1上,且B1D∶DC1=1∶3.
(Ⅰ)证明:BD⊥A1C;
(Ⅱ)若二面角B-A1D-B1的大小为60º,试求a的值.
将3个完全相同的小球随机地放入编号依次为1,2,3,4,5的盒子里,用随机变量 表示有球盒子编号的最大值.
表示有球盒子编号的最大值.
(Ⅰ)求 ;
;
(Ⅱ)求 的分布列和数学期望
的分布列和数学期望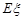 .
.