以下是某地搜集到的新房屋的销售价格 和房屋的面积
和房屋的面积 的数据:
的数据:
房屋面积 |
110 |
90 |
80 |
100 |
120 |
| 销售价格(万元) |
33 |
31 |
28 |
34 |
39 |
(1)画出数据对应的散点图;
(2)求线性回归方程;
(3)据(2)的结果估计当房屋面积为 时的销售价格.
时的销售价格.
(提示: ,
,  ,
, ,
, )
)
已知抛物线C关于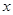 轴对称,它的顶点在坐标原点,并且经过点
轴对称,它的顶点在坐标原点,并且经过点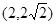
(1)求抛物线C的标准方程
(2)直线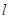 过抛物线的焦点F,与抛物线交于A、B两点,线段AB的中点M的横坐标为3,求弦长
过抛物线的焦点F,与抛物线交于A、B两点,线段AB的中点M的横坐标为3,求弦长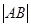 以及直线
以及直线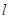 的方程。
的方程。
已知曲线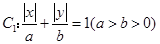 所围成的封闭图形的面积为
所围成的封闭图形的面积为 ,曲线
,曲线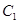 的内切圆半径为
的内切圆半径为 .记
.记 为以曲线
为以曲线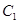 与坐标轴的交点为顶点的椭圆.
与坐标轴的交点为顶点的椭圆.
(1)求椭圆 的标准方程;
的标准方程;
(2)设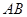 是过椭圆
是过椭圆 中心的任意弦,
中心的任意弦, 是线段
是线段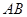 的垂直平分线.
的垂直平分线. 是
是 上异于椭圆中心的点.
上异于椭圆中心的点.
(i)若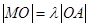 (
(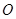 为坐标原点),当点
为坐标原点),当点 在椭圆
在椭圆 上运动时,求点
上运动时,求点 的轨迹方程;
的轨迹方程;
(ii)若 是
是 与椭圆
与椭圆 的交点,求
的交点,求 的面积的最小值.
的面积的最小值.
命题p:  ,其中
,其中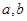 满足条件:五个数
满足条件:五个数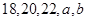 的平均数是20,标准差是
的平均数是20,标准差是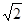 ; 命题q:m≤t≤n ,其中m,n满足条件:点M在椭圆
; 命题q:m≤t≤n ,其中m,n满足条件:点M在椭圆 上,定点A(1,0),m、n分别为线段AM长的最小值和最大值。若命题“p或q”为真且命题“p且q”为假,求实数t的取值范围。
上,定点A(1,0),m、n分别为线段AM长的最小值和最大值。若命题“p或q”为真且命题“p且q”为假,求实数t的取值范围。
如图,已知圆O的直径AB=4,定直线L到圆心的距离为4,且直线L⊥直线AB。点P是圆O上异于A、B的任意一点,直线PA、PB分别交L与M、N点。试建立适当的直角坐标系,解决下列问题: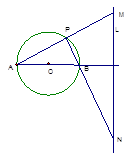
(1)若∠PAB=30°,求以MN为直径的圆方程;
(2)当点P变化时,求证:以MN为直径的圆必过圆O内的一定点。
已知抛物线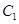 的顶点在坐标原点,它的准线经过双曲线
的顶点在坐标原点,它的准线经过双曲线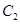 :
: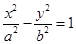 的一个焦点
的一个焦点 且垂直于
且垂直于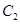 的两个焦点所在的轴,若抛物线
的两个焦点所在的轴,若抛物线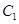 与双曲线
与双曲线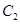 的一个交点是
的一个交点是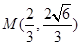 .
.
(1)求抛物线 的方程及其焦点
的方程及其焦点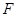 的坐标;
的坐标;
(2)求双曲线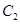 的方程及其离心率
的方程及其离心率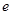 .
.