如图，在四棱锥
中，
平面
，底面
是菱形，
，
．
（Ⅰ）求证：
；
（Ⅱ）若
，求二面角
的余弦值.
做投掷2颗骰子的试验，用（x，y）表示结果，其中x表示第1颗骰子出现的点数，y 表示第2颗骰子出现的点数，写出：
（1）求事件“出现点数相等”的概率（2）求事件“出现点数之和大于8”的概率。
某射手在一次射击训练中，射中10环，9环，8环、7环的概率分别是0.21，0.23，0.25，0.28，计算这个射手在一次射击中：
（1）射中10环或7环的概率；（2）不够7环的概率。
设两个非零向量
不共线.
(1)
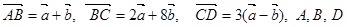三点是否能构成三角形, 并说明理由.
(2)试确定实数k, 使
已知数列
为等差数列，且
（１）求数列
的通项公式；(2)求数列的前n项和
。
已知：
，当
时，
；
时，
（1）求
的解析式.
（2）c为何值时，
的解集为R.