设函数f(x)在R上是偶函数,在区间(-∞,0)上递增,且f(2a2+a+1)<f(2a2-2a+3),求a的取值范围.
如图:四棱锥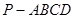 中,底面
中,底面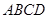 是平行四边形,且
是平行四边形,且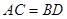 ,
,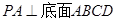 ,
,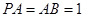 ,
,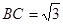 ,点
,点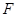 是
是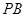 的中点,点
的中点,点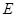 在边
在边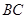 上移动.
上移动.
(1)证明:当点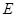 在边
在边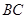 上移动时,总有
上移动时,总有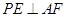 ;
;
(2)当 等于何值时,
等于何值时,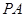 与平面
与平面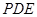 所成角的大小为45°.
所成角的大小为45°.
某厂采用新技术改造后生产甲产品的产量x(吨)与相应的生产成本y(万元)的几组对照数据.
| x |
3 |
4 |
5 |
6 |
| y |
3 |
3.5 |
4.5 |
5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程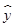 =
=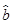 x+
x+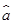 ;
;
(3)已知该厂技改前生产50吨甲产品的生产成本为40万元.试根据(2)求出的线性回归方程,预测生产50吨甲产品的生产成本比技改前降低多少万元?
(参考数据: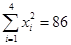

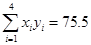 ,
,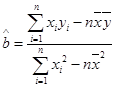 )
)
设关于 的一元二次方程
的一元二次方程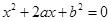 .
.
(1)若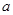 是从1,2,3,4四个数中任取的一个数,
是从1,2,3,4四个数中任取的一个数,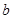 是从0,1,2三个数中任取的一个数,求上述方程有两个不等实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有两个不等实根的概率;
(2)若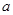 是从区间
是从区间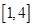 任取的一个数,
任取的一个数,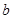 是从区间
是从区间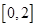 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
在平面直角坐标系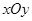 中,圆
中,圆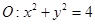 交
交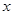 轴于点
轴于点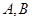 (点
(点 在
在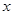 轴的负半轴上),点
轴的负半轴上),点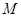 为圆
为圆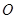 上一动点,
上一动点,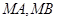 分别交直线
分别交直线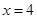 于
于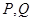 两点.
两点.
(1)求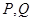 两点纵坐标的乘积;
两点纵坐标的乘积;
(2)若点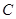 的坐标为
的坐标为 ,连接
,连接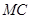 交圆
交圆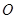 于另一点
于另一点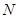 ,
,
①试判断点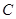 与以
与以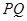 为直径的圆的位置关系,并说明理由;
为直径的圆的位置关系,并说明理由;
②记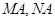 的斜率分别为
的斜率分别为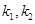 ,试探究
,试探究 是否为定值?若是,请求出该定值;若不是,请说明理由.
是否为定值?若是,请求出该定值;若不是,请说明理由.
如图,已知四边形 和
和 都是菱形,平面
都是菱形,平面 和平面
和平面 互相垂直,且
互相垂直,且 .
.
(Ⅰ)求证:
(Ⅱ)求四面体 的体积.
的体积.