设 ,其中
,其中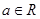 .
.
(1)若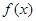 有极值,求
有极值,求 的取值范围;
的取值范围;
(2)若当 ,
,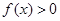 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(本小题满分12分)为迎接国庆60周年,美化城市,某市将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,如图所示。要求B在AM上,D在AN上,且对角线MN过C点,|AB|=3米,|AD|=2米.
(I)要使矩形AMPN的面积大于32平方米,则AN的长应在什么范围内? (Ⅱ)若AN的长度不小于6米,则当AM、AN的长度是多少时,矩形AMPN的面积最小并求出最小面积.
(Ⅱ)若AN的长度不小于6米,则当AM、AN的长度是多少时,矩形AMPN的面积最小并求出最小面积.
(本小题满分13分)已知函数 ,.
,.
(Ⅰ) 求函数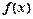 在点(1,
在点(1, )处的切线方程;(Ⅱ) 若函数
)处的切线方程;(Ⅱ) 若函数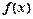 与
与 在区间
在区间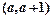 上均为增函数,求
上均为增函数,求 的取值范围;(Ⅲ) 若方程
的取值范围;(Ⅲ) 若方程 有唯一解,试求实数
有唯一解,试求实数 的值.
的值.
给出三条直线 ,
,
(1)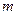 为何值时,三线共点;
为何值时,三线共点;
(2) 时,三条直线能围成一个三角形吗?
时,三条直线能围成一个三角形吗?
(3)求当三条直线围成三角形时,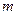 的取值范围.
的取值范围.
已知点 ,
,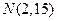 .在直线
.在直线 上的找一点
上的找一点 ,使
,使 最小,并求出最小值.
最小,并求出最小值.
在一个平面上,机器人到与点 距离为
距离为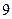 的地方绕
的地方绕 点顺时针而行,在行进过程中保持与点
点顺时针而行,在行进过程中保持与点 的距离不变.它在行进过程中到经过点
的距离不变.它在行进过程中到经过点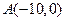 与
与 的直线的最近距离和最远距离分别是多少?
的直线的最近距离和最远距离分别是多少?