已知 是椭圆
是椭圆 上一点,且点
上一点,且点 到椭圆的两个焦点距离之和为
到椭圆的两个焦点距离之和为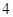 ;
;
(1)求椭圆方程;
(2)设 为椭圆的左顶点,直线
为椭圆的左顶点,直线 交
交 轴于点
轴于点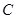 ,过
,过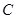 作斜率为
作斜率为 的直线
的直线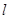 交椭圆于
交椭圆于 两点,若
两点,若 ,求实数
,求实数 的值.
的值.
已知函数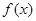
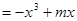 在
在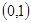 上是增函数
上是增函数
(1)求实数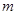 的取值集合
的取值集合
(2)当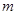 取值集合
取值集合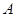 中的最小值时, 定义数列
中的最小值时, 定义数列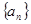 ;满足
;满足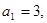 且
且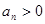 ,
,  , 设
, 设 , 证明:数列
, 证明:数列 是等比数列, 并求数列
是等比数列, 并求数列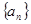 的通项公式.
的通项公式.
(3)若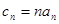 , 数列
, 数列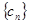 的前
的前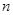 项和为
项和为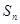 , 求
, 求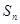 .
.
如图, 三棱柱ABC—A1B1C1的侧棱AA1⊥底面ABC, ∠ACB =" 90°," E是棱CC1上动点, F是AB中点, AC =" 1," BC =" 2," AA1 =" 4." 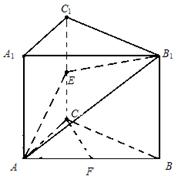
(1) 当E是棱CC1中点时, 求证: CF∥平面AEB1;
(2) 在棱CC1上是否存在点E, 使得二面角A—EB1—B
的余弦值是 , 若存在, 求CE的长, 若不存在,
, 若存在, 求CE的长, 若不存在,
请说明理由.
某网站用“10分制”调查一社区人们的幸福度.现从调查人群中随机抽取16名, 以下茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎, 小数点后的一位数字为叶):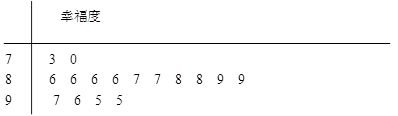
(1) 指出这组数据的众数和中位数;
(2) 若幸福度不低于9.5分, 则称该人的幸福度为“极幸福”.求从这16人中随机选取3人, 至多有1人是“极幸福”的概率;
(3) 以这16人的样本数据来估计整个社区的总体数据, 若从该社区(人数很多)任选3人, 记 表示抽到“极幸福”的人数, 求
表示抽到“极幸福”的人数, 求 的分布列及数学期望.
的分布列及数学期望.
已知锐角△ABC的三内角A、B、C的对边分别是a、b、c, 且(b2+c2-a2)tanA= bc.
bc.
(1)求角A的大小;
(2)求sin(A+10°)·[1- tan(A-10°)]的值.
tan(A-10°)]的值.
在极坐标中,已知圆 经过点
经过点 ,圆心为直线
,圆心为直线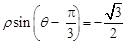 与极轴的交点,求圆
与极轴的交点,求圆 的极坐标方程.
的极坐标方程.