某网站用“10分制”调查一社区人们的幸福度.现从调查人群中随机抽取16名, 以下茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎, 小数点后的一位数字为叶)：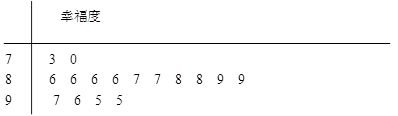
(1) 指出这组数据的众数和中位数；
(2) 若幸福度不低于9.5分, 则称该人的幸福度为“极幸福”.求从这16人中随机选取3人, 至多有1人是“极幸福”的概率；
(3) 以这16人的样本数据来估计整个社区的总体数据, 若从该社区(人数很多)任选3人, 记
表示抽到“极幸福”的人数, 求的分布列及数学期望．
右面的图形无限向内延续，最外面的正方形的边长等1。从外到内，第i个正方形与内切圆之间的深灰色图形面积记为Si（i="1," 2, …）。
分别求S1，S2，Sk；
求深灰色图形的面积的总和。
如图，四边形ABCD为矩形，DA⊥平面ABE，
AE=EB=BC=2，EB⊥平面ACE于点F，且点F在CE上。
（1）求证：AE⊥BE；（2）求三棱锥D—AEC的体积；
（3）设点M在线段AB上，且满足AM=2MB，试在线段CE上确定一点N，使得MN//平面DAE。
已知圆
（1）求过点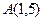
的圆C的切线方程；
（2）求在两坐标轴上截距之和为0，且截圆C所得弦长为2的直线方程。
已知集合
（1）若
，求实数m的值；（2）若
，求实数m的取值范围.
设数列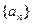
的通项公式为
。数列
定义如下：对于正整数m，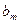
是使得不等式
成立的所有n中的最小值。（1）若
，求b3；（2）若
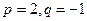，求数列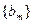
的前2m项和公式；（3）是否存在p和q，使得
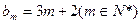？如果存在，求p和q的取值范围；如果不存在，请说明理由。