已知锐角△ABC的三内角A、B、C的对边分别是a、b、c, 且(b2+c2-a2)tanA= bc.
bc.
(1)求角A的大小;
(2)求sin(A+10°)·[1- tan(A-10°)]的值.
tan(A-10°)]的值.
(本小题满分10分)如图,四棱锥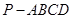 中,
中,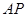 ⊥平面
⊥平面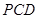 ,
,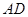 ∥
∥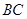 ,
,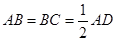 ,
,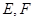 分别为线段
分别为线段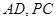 的中点.
的中点.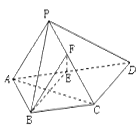
(1)求证: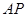
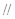 平面
平面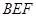 ;
;
(2)求证: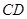 ⊥平面
⊥平面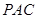 .
.
(本小题满分13分)已知△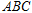 的两个顶点
的两个顶点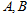 的坐标分别是
的坐标分别是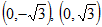 ,且
,且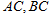 所在直线的斜率之积等于
所在直线的斜率之积等于 .
.
(1)求顶点 的轨迹
的轨迹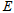 的方程,并判断轨迹
的方程,并判断轨迹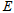 为何种曲线;
为何种曲线;
(2)当 时,点
时,点 为曲线 C上点,且点
为曲线 C上点,且点 为第一象限点,过点
为第一象限点,过点 作两条直线与曲线C交于
作两条直线与曲线C交于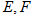 两点,直线
两点,直线 斜率互为相反数,则直线EF斜率是否为定值,若是,求出定值,若不是,请说明理由.
斜率互为相反数,则直线EF斜率是否为定值,若是,求出定值,若不是,请说明理由.
(本小题满分13分)如图,椭圆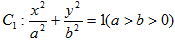 的离心率为
的离心率为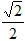 ,
,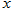 轴被曲线
轴被曲线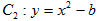 截得的线段长等于
截得的线段长等于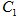 的短轴长.
的短轴长.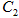 与
与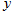 轴的交点为M,过坐标原点O的直线
轴的交点为M,过坐标原点O的直线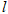 与
与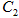 相交于点A、B.
相交于点A、B.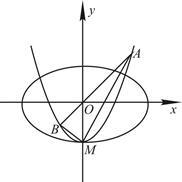
(1)求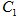 ,
,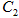 的方程;
的方程;
(2)求证:MA⊥MB.
(本小题满分12分)如图四边形ABCD为菱形,G为AC与BD交点, ,
,
(1)证明:平面 平面
平面 ;
;
(2)若 ,
,
 ,令AE与平面ABCD所成角为
,令AE与平面ABCD所成角为 ,且
,且 ,求该四棱锥
,求该四棱锥 的体积.
的体积.
(本小题满分12分)已知双曲线 ,若双曲线的渐近线过点
,若双曲线的渐近线过点 ,且双曲线过点
,且双曲线过点
(1) 求双曲线 的方程;
的方程;
(2)若双曲线 的左、右顶点分别为
的左、右顶点分别为 ,点
,点 在
在 上且直线
上且直线 的斜率的取值范围是
的斜率的取值范围是 ,求直线
,求直线 斜率的取值范围.
斜率的取值范围.