(本小题满分13分)已知△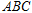 的两个顶点
的两个顶点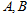 的坐标分别是
的坐标分别是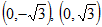 ,且
,且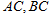 所在直线的斜率之积等于
所在直线的斜率之积等于 .
.
(1)求顶点 的轨迹
的轨迹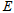 的方程,并判断轨迹
的方程,并判断轨迹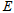 为何种曲线;
为何种曲线;
(2)当 时,点
时,点 为曲线 C上点,且点
为曲线 C上点,且点 为第一象限点,过点
为第一象限点,过点 作两条直线与曲线C交于
作两条直线与曲线C交于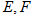 两点,直线
两点,直线 斜率互为相反数,则直线EF斜率是否为定值,若是,求出定值,若不是,请说明理由.
斜率互为相反数,则直线EF斜率是否为定值,若是,求出定值,若不是,请说明理由.
(本小题满分12分)已知锐角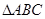 中内角
中内角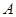 、
、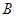 、
、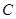 的对边分别为
的对边分别为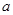 、
、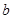 、
、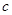 ,且
,且 .
.
(1)求角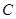 的值;
的值;
(2)设函数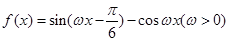 ,
,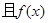 图象上相邻两最高点间的距离为
图象上相邻两最高点间的距离为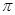 ,求
,求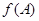 的取值范围.
的取值范围.
(本小题满分12分)如图所示,四棱锥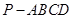 中,
中,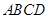 为正方形,
为正方形,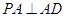
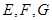 分别是线段
分别是线段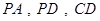 的中点. 求证:
的中点. 求证:
(1)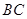 //平面
//平面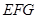 ;
;
(2)平面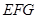 ⊥平面
⊥平面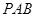 .
.
(本小题满分12分)已知函数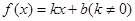 的图象与
的图象与 轴分别相交于点
轴分别相交于点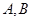 两点,向量
两点,向量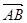
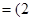 ,
,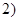 ,又函数
,又函数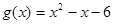 ,且
,且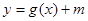 的值域是
的值域是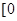 ,
,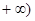 。
。
(1)求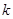 ,
,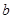 及
及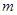 的值;(2)当
的值;(2)当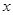 满足
满足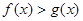 时,求函数
时,求函数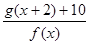 的最小值。
的最小值。
已知函数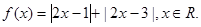 .
.
(Ⅰ)解不等式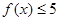 ;
;
(Ⅱ)若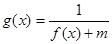 的定义域为
的定义域为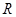 ,求实数
,求实数 的取值范围.
的取值范围.
已知极坐标的极点与平面直角坐标系的原点重合,极轴与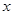 轴的正半轴重合,且长度单位相同.圆
轴的正半轴重合,且长度单位相同.圆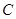 的参数方程为
的参数方程为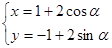 (
( 为参数),点
为参数),点 的极坐标为
的极坐标为 .(Ⅰ)化圆
.(Ⅰ)化圆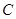 的参数方程为极坐标方程;(Ⅱ)若点
的参数方程为极坐标方程;(Ⅱ)若点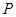 是圆
是圆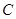 上的任意一点, 求
上的任意一点, 求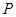 ,
, 两点间距离的最小值.
两点间距离的最小值.