先后抛掷三枚均匀的硬币，至少出现一次正面的概率是 .
从甲地到乙地，须经丙地，从甲地到丙地有4条路，从丙地到乙地有2条路，从甲地到乙地有▲条不同的路线．
（本小题满分12分）
已知函数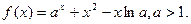
（I）求证：函数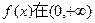
上单调递增；
（II）若方程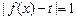
有三个不同的实根，求t的值；
（III）对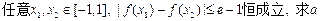
的取值范围。
（本小题满分12分）
设点M、N分别是不等边△ABC的重心与外心，已知
、
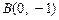，且
.
（1）求动点C的轨迹E；
（2）若直线
与曲线E交于不同的两点P、Q，且满足
，求实数
的取值范围。
（本小题满分12分）
已知函数
在[0，+
）上最小值是
（1）求数列
的通项公式；
（2）令
，求证：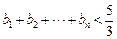
；
（本小题满分12分）
如图甲，直角梯形ABCD中，AB∥CD，，点M、N分别在AB、CD上，且MN⊥AB，MC⊥CB，BC＝2，MB＝4，现将梯形ABCD沿MN折起，使平面AMND与平面MNCB垂直（如图乙）
（1）求证：AB∥平面DNC；
（2）当DN的长为何值时，二面角D－BC－N的大小为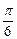
？