如图,某几何体的下部分是长为8,宽为6,高为3的长方体,上部分是侧棱长都相等且高为3的四棱锥,求:
(1)该几何体的体积;
(2)该几何体的表面积.
(本小题满分16分)
 点,点A1(x1,0),A2(x
点,点A1(x1,0),A2(x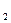 ,0),…,An(xn,0),…顺次为x轴上的点,其中x1=a(0<a≤1).对于任意n∈N*,点An、Bn、An+1构成以Bn为顶点的等腰三角形.(1)求数列{yn}的通项公式,并证明它为等差数列;(2)求证:x
,0),…,An(xn,0),…顺次为x轴上的点,其中x1=a(0<a≤1).对于任意n∈N*,点An、Bn、An+1构成以Bn为顶点的等腰三角形.(1)求数列{yn}的通项公式,并证明它为等差数列;(2)求证:x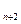 - x
- x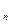 是常数,并求数列{ x
是常数,并求数列{ x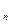 }的通项公式;(3)上述等腰ΔAnBnAn+1中是否可能存在直角三角形,若可能,求出此时a的值;若不可能,请说明理由.
}的通项公式;(3)上述等腰ΔAnBnAn+1中是否可能存在直角三角形,若可能,求出此时a的值;若不可能,请说明理由.
(本小题满分14分)已知函数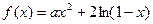 (
(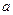 为实数).
为实数).
(I)若 在
在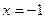 处有极值,求
处有极值,求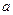 的值;(II)若
的值;(II)若 在
在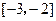 上是增函数,求
上是增函数,求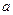 的取值范围.
的取值范围.
(本小题满分14分)已知: 为常数)
为常数)
(1)若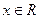 ,求
,求 的最小正周期;(2)若
的最小正周期;(2)若 在[
在[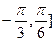 上最大值与最小值之和为5,求
上最大值与最小值之和为5,求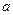 的值;(3)在(2)条件下
的值;(3)在(2)条件下 先按
先按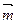 平移后再经过伸缩变换后得到
平移后再经过伸缩变换后得到 求
求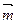 .
.
(矩阵与变换)
二阶矩阵M对应的变换将点(1,-1)与(-2,1)分别变换成点(-1,-1)与(0,-2).
(Ⅰ) 求矩阵M; (Ⅱ) 设直线l在变换M作用下得到了直线m:x-y=4,求l的方程.
(本小题满分10分) 如图A,B两点之间有6条网线并联,它们能通过的最大信息量分别为1,1,2,2,3,4.现从中任取三条网线且使每条网线通过最大的信息量.
如图A,B两点之间有6条网线并联,它们能通过的最大信息量分别为1,1,2,2,3,4.现从中任取三条网线且使每条网线通过最大的信息量.
(1)设选取的三条网线由A到B可通过的信息
总量为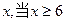 时,则保证信息畅通.
时,则保证信息畅通.
求线路信息畅通的概率;
(2)求选取的三条网线可通过信息总量的数学期望.