(本小题满分12分)
某工厂生产 两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
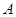 |
7 |
7 |
7.5 |
9 |
9.5 |
 |
6 |
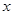 |
8.5 |
8.5 |
 |
由于表格被污损,数据 看不清,统计员只记得
看不清,统计员只记得 ,且
,且 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等.
(Ⅰ)求表格中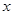 与
与 的值;
的值;
(Ⅱ)若从被检测的5件 种元件中任取2件,求2件都为正品的概率.
种元件中任取2件,求2件都为正品的概率.
(本小题满分14分)已知椭圆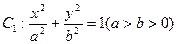 ,它的离心率为
,它的离心率为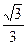 ,直线
,直线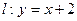 与以原点为圆心,以椭圆
与以原点为圆心,以椭圆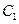 的短半轴长为半径的圆相切.⑴求椭圆
的短半轴长为半径的圆相切.⑴求椭圆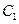 的方程;⑵设椭圆
的方程;⑵设椭圆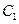 的左焦点为
的左焦点为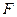 ,左准线为
,左准线为 ,动直线
,动直线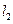 垂直于直线
垂直于直线 ,垂足为点
,垂足为点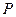 ,线段
,线段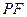 的垂直平分线交
的垂直平分线交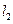 于点
于点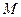 ,求动点
,求动点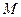 的轨迹
的轨迹 的方程;⑶将曲线
的方程;⑶将曲线 向右平移2个单位得到曲线
向右平移2个单位得到曲线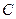 ,设曲线
,设曲线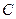 的准线为
的准线为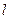 ,焦点为
,焦点为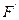 ,过
,过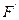 作直线
作直线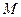 交曲线
交曲线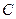 于
于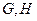 两点,过点
两点,过点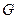 作平行于曲线
作平行于曲线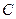 的对称轴的直线
的对称轴的直线 ,若
,若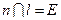 ,试证明三点
,试证明三点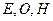 (
(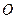 为坐标原点)在同一条直线上.
为坐标原点)在同一条直线上.
(本小题满分12分)等差数列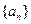 的前
的前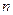 项和为
项和为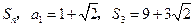 .
.
⑴求数列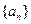 的通项
的通项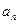 与前
与前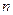 项和
项和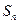 ;⑵设
;⑵设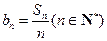 ,求证:数列
,求证:数列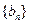 中任意不同的三项都不可能成为等比数列.
中任意不同的三项都不可能成为等比数列.
(本小题满分12分)在四边形ABCD中, BD是它的一条对角线,且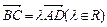 ,
,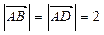 ,
, .⑴若△BCD是直角三形,求
.⑴若△BCD是直角三形,求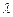 的值;⑵在⑴的条件下,求
的值;⑵在⑴的条件下,求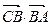 .
.
(本小题满分12分)
如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
⑴证明PA//平面EDB; ⑵证明PB⊥平面EFD;
⑵证明PB⊥平面EFD;
⑶求二面角C—PB—D的大小.
已知函数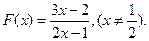

(1)求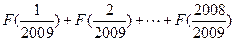 的值;
的值;
(2)已知数列 ,求数列
,求数列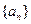 的通项公式;
的通项公式;
(3)求证: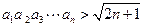 .
.