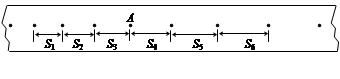(1)“测定匀变速直线运动的加速度”的实验中,具体测算加速度前的主要步骤有:
| A.将打点计时器固定在长木板上没有滑轮的一端,接上低压交流电源; |
| B.把纸带固定在小车后端并让纸带穿过打点计时器; |
| C.把一条细绳拴在小车前端,绳跨过滑轮挂上砝码; |
| D.把小车停在靠近打点计时器的地方,先放开小车,再接通电源; |
E、断开电源,取下纸带;
F、换上纸带重复做三次,选择一条较为理想的纸带;
以上步骤有错误的是( )
(2)一同学在练习使用电磁打点计时器时,打出3条纸带(ab间距离相等),则______条纸带的平均速度大,_________纸带的加速度为零。
(3)在“探究小车速度随时间变化的规律”的实验中,如图给出了从0点开始,每5个点取一个计数点的纸带,其中0、1、2、3、4、5、6都为计数点,测得:
x1=1.40cm, x2=1.90cm, x3=2.38cm, x4=2.88cm, x5=3.39cm, x6=3.87cm.那么:(保留两位有效数字)
① 在计时器打出点1、2、3、4、5时,小车的速度分别为:
v1=_______ m/s,
v2=______ m/s,
v3=______ m/s,
v4=_______m/s,
v5=________m/s.
② 在平面直角坐标系中作出v-t图象.
图象可得小车的加速度大小a=________m/s2。
在探究求合力的方法时,先将橡皮条的一端固定在水平木板上,另一端系上带有绳套的绳套两根细绳。实验时,需要两次拉伸橡皮条,一次是通过两细绳用两个弹簧秤互成角度地拉橡皮条,另一次是用一个弹簧秤通过细绳拉橡皮条。
(1)实验对两次拉伸橡皮条的要求中,下列哪些说法是正确的__________(填字母代号)
A.将橡皮条拉伸相同长度即可
B.将橡皮条沿相同方向拉到相同长度
C.将弹簧秤都拉伸到相同刻度
D.将橡皮条和细绳的结点拉到相同位置
(2)同学们在操作过程中有如下议论,其中对减小实验误差有益的说法是_______(填字母代号)
A.两细绳必须等长
B.弹簧秤、细绳、橡皮条都应与木板平行
C.用两弹簧秤同时拉细绳时两弹簧秤示数之差应尽可能大
D.拉橡皮条的细绳要长些,标记同一细绳方向的两点要远些
在《验证力的平行四边形定则》实验中,某同学首先将白纸固定在方木板上、将橡皮筋的一端固定在A点,另一端拴上两根细绳,每根细绳分别连着一个量程为5 N、最小刻度为0.1 N的弹簧测力计.然后沿着两个不同的方向拉弹簧测力计,如图所示,夹角约为900,这时必须在白纸上记下两拉力的大小和方向,还必须记下 ,其中右图中B弹簧测力计的读数为N。接着,用其中一个弹簧测力计去拉该橡皮筋时,该实验能否顺利进行下去 吗?请说明理由。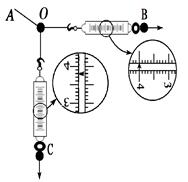
某同学用打点计时器测量做匀加速直线运动的物体的加速度,电源频率f="50" Hz在纸带上打出的点中,选出零点,每隔4个点取1个计数点,因保存不当,纸带被污染,如图所示,A、B、C、D是依次排列的4个计数点,仅能读出其中3个计数点到零点的距离: ,
, ,
,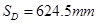

若无法再做实验,可由以上信息推知:
①相邻两计数点的时间间隔为__________s
②打C点时物体的速度大小为___________m/s(取2位有效数字)
③物体的加速度大小为__________m/s2
在探究力的合成方法时,先将橡皮条的一端固定在水平木板上,另一端系上带有绳套的两根细绳。实验时,需要两次拉伸橡皮条,一次是通过两细绳用两个弹簧秤互成角度地拉橡皮条,另一次是用一个弹簧秤通过细绳拉橡皮条。
①实验对两次拉伸橡皮条的要求中,下列哪些说法是正确的(填字母代号)
A.将橡皮条拉伸相同长度即可
B. 将弹簧秤都拉伸到相同刻度
C. 将橡皮条沿相同方向拉到相同长度
D.将橡皮条和绳的结点拉到相同位置
②同学们在操作过程中有如下议论,其中对减小实验误差有益的说法是 (填字母代号)
A.拉橡皮条的细绳要适当长些,标记同一细绳方向的两点要适当远些
B.弹簧秤、细绳、橡皮条都应与木板平行
C.用两弹簧秤同时拉细绳时两弹簧秤示数之差应尽可能大
D.两细绳必须等长
如图所示,某同学在做“研究匀变速直线运动”实验中,由打点计时器得到表示小车运动过程的一条清晰纸带,纸带上两相邻计数点的时间间隔为T=0.10s,其中S1=7.05cm、S2=7.68cm、S3=8.33cm、S4=8.95cm、S5=9.61cm、S6=10.26cm,则A点处瞬时速度的大小是_______m/s,小车运动的加速度计算表达式为_______ ,加速度的大小是_______m/s2(计算结果保留两位有效数字)。