某市采用价格调控的手段达到节约用水的目的,制定如下用水收费标准:每户每月用水不超过6m3,水费按a元/m3收费;若超过6m3,6m3以内的仍按a元/m3收费,超过6m3的部分以b元/m3收费.某户居民5、6月份用水量和水费如下表:
| 月份 |
用水量(m3) |
水费(元) |
| 5 |
5 |
7.5 |
| 6 |
9 |
27 |
设该用户每月用水量为xm3,应交水费y元.
(1)求出a,b的值;
(2)写出用水量不超过6m3和超过6m3时,y与x之间的函数关系式;
(3)若该用户7月份用水量为8m3,他应交多少元水费?
如图,CA、CB为⊙O的切线,切点分别为A、B.直径延长AD与CB的延长线交于点E.AB、CO交于点M,连接OB.
(1)求证:∠ABO=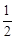 ∠ACB;
∠ACB;
(2)若sin∠EAB= ,CB=12,求⊙O 的半径及
,CB=12,求⊙O 的半径及 的值.
的值.
据报道,历经一年半的调查研究,北京PM 2.5源解析已经通过专家论证.各种调查显示,机动车成为PM 2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天至少就要向大气里排放0.035千克污染物.以下是相关的统计图、表:
(1)请根据所给信息补全扇形统计图;
(2)请你根据“2013年北京市全年空气质量等级天数统计表”计算该年度重度污染和严重污染出现的频率共是多少?(精确到0.01)
(3)小明是社区环保志愿者,他和同学们调查了本社区的100辆机动车,了解到其中每天出行超过20千米的有40辆.已知北京市2013年机动车保有量已突破520万辆,请你通过计算,估计2013年北京市一天中出行超过20千米的机动车至少要向大气里排放多少千克污染物?
如图,△ABC中,BC >AC,点D在BC上,且CA=CD,∠ACB的平分线交AD于点F,E是AB的中点.
(1)求证:EF∥BD ;
(2)若∠ACB=60°,AC=8,BC=12,求四边形BDFE的面积.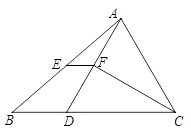
列方程或方程组解应用题:
从A地到B地有两条行车路线:
路线一:全程30千米,但路况不太好;
路线二:全程36千米,但路况比较好,一般情况下走路线二的平均车速是走路线一的
平均车速的1.8倍,走路线二所用的时间比走路线一所用的时间少20分钟.
那么走路线二的平均车速是每小时多少千米?
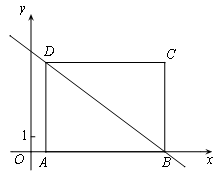
如图,在平面直角坐标系xOy中,矩形ABCD的边AD=6,A(1,0), B(9,0),直线y=kx+b经过B、D两点.
(1)求直线y=kx+b的表达式;
(2)将直线y=kx+b平移,当它与矩形没有公共点时,直接写出b的取值范围.