阅读下列解答过程,并回答问题.
在(x2+ax+b)(2x2﹣3x﹣1)的积中,x3项的系数为﹣5,x2项的系数为﹣6,求a,b的值.
解:(x2+ax+b)•(2x2﹣3x﹣1)=
2x4﹣3x3+2ax3+3ax2﹣3bx=①
2x4﹣(3﹣2a)x3﹣(3a﹣2b)x2﹣3bx ②
根据对应项系数相等,有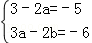 ,解得
,解得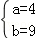
回答:
(1)上述解答过程是否正确? .
(2)若不正确,从第 步开始出现错误,其他步骤是否还有错误? .
(3)写出正确的解答过程.
解方程
如图, 四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4). 点 从
从 出发以每秒2个单位长度的速度向
出发以每秒2个单位长度的速度向 运动;点
运动;点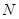 从
从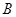 同时出发,以每秒1个单位长度的速度向
同时出发,以每秒1个单位长度的速度向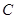 运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点
运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点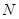 作
作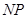 垂直
垂直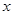 轴于点
轴于点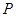 ,连结AC交NP于Q,连结MQ.
,连结AC交NP于Q,连结MQ. 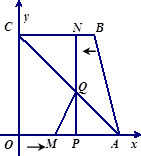
点(填M或N)能到达终点;
求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大;
是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标,若不存在,
说明理由.

如图①,以点M(-1,0)为圆心的圆与y轴、x轴分别交于点A、B、C、D,直线y=-x-与⊙M相切于点H,交x轴于点E,交y轴于点F.请直接写出OE、⊙M的半径r、CH的长;
如图②,弦HQ交x轴于点P,且DP:PH=3:2,求cos∠QHC的值;
如图③,点K为线段EC上一动点(不与E、C重合),连接BK交⊙M于点T,弦AT交x轴于点N.是否存在一个常数a,始终满足MN·MK=a,如果存在,请求出a的值;如果不存在,请说明理由.
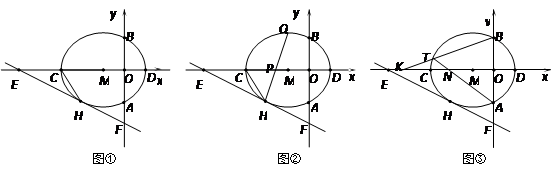
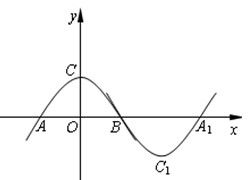
如图所示,抛物线m:y=ax2+b(a<0,b>0)与x轴于点A、B(点A在点B的左侧),与y轴交于点C.将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为C1,与x轴的另一个交点为A1.当a=-1 , b=1时,求抛物线n的解析式;
四边形AC1A1C是什么特殊四边形,请写出结果并说明理由;
若四边形AC1A1C为矩形,请求出a和b应满足的关系式.

为了保证中小学学生上下学的安全,某县根据实际需要计划购买大、中型两种校车共20辆,已知大型校车每辆62万元,中型校车每辆40万元,设购买大型校车x(辆),购车总费用为y(万元).求y与x的函数关系式(不要求写出自变量x的取值范围);
若购买中型校车的数量少于大型校车的数量,请你给出一种费用最省的方案,
并求出该方案所需费用.