如图1，点C将线段AB分成两部分，如果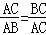
，那么称点C为线段AB的黄金分割点．某研究小组在进行课题学习时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S1，S2，如果
，那么称直线l为该图形的黄金分割线．
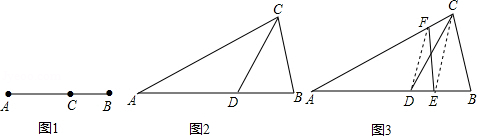
（1）研究小组猜想：在△ABC中，若点D为AB边上的黄金分割点（如图2），则直线CD是△ABC的黄金分割线．你认为对吗？为什么？
（2）研究小组在进一步探究中发现：过点C任作一条直线交AB于点E，再过点D作直线DF∥CE，交AC于点F，连接EF（如图3），则直线EF也是△ABC的黄金分割线．请你说明理由．
在解关于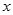
，
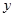的方程组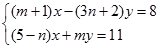
时，可以用 ①×2－②消去未知数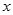；也可以用①＋②×5消去未知数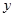，试求
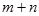的值.
计算
（1）
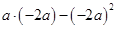
（2）
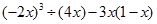
（3）
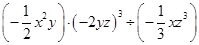
如图，点E在直线DF上，点B在直线AC上，若∠1＝∠2，∠3＝∠4，则∠A＝∠F，请说明理由．
解：∵∠1＝∠2（已知），∠2＝∠DGF（）
∴∠1＝∠DGF
∴BD∥CE（）
∴∠3＋∠C＝180º（）
又∵∠3＝∠4（已知）
∴∠4＋∠C＝180º
∴ ∥ （同旁内角互补，两直线平行）
∴∠A＝∠F（）
某步行街摆放有若干盆甲、乙、丙三种造型的盆景．甲种盆景由15朵红花、24朵黄花和25朵紫花搭配而成；乙种盆景由10朵红花、12朵黄花搭配而成；丙种盆景由10朵红花、18朵黄花和25朵紫花搭配而成．这些盆景一共用了2900朵红花，3750朵紫花，则黄花一共用了朵．
如图，在△ABC中，∠B=90°，AB=6cm，BC=8cm，点P、Q为AB边及BC边上的两个动点。（1）若点P从点A沿AB边向点B以1cm/s的速度移动，与此同时，点Q从点B开始沿BC边向点C以2cm/s的速度移动，两个点同时出发。
①经过几秒，△PBQ的面积等于8cm2；
②是否存在这样的时刻，使△PBQ的面积等于10 cm2？如果存在请求出来，如果不存在，请说明理由。
（2）假设点P、Q可以分别在AB、BC边上任意移动，是否存在PQ同时平分△ABC的周长和面积的情况？如果存在请求出BP的长度；如果不存在，请说明理由。