已知:a+b=3,ab=2,求下列各式的值:
(1)a2b+ab2(2)a2+b2
某学校为改善老师的办公条件,计划购买若干台电脑,现从两个电脑城了解到某品牌同一型号的电脑每台标价都是4000元,但学校集体购买都有一定的优惠.
甲电脑城的优惠方法是:第一台按标价收费,其余每台可优惠15%.则甲电脑城的总收费y1(元)与学校所买电脑的台数x之间的关系式是.
乙电脑城的优惠方法是:每台都优惠12%.则乙电脑城的总收费y2(元)与学校所买电脑的台数x之间的关系式是.
⑴学校在什么情况下到甲电脑城购买更优惠?
⑵学校在什么情况下到乙电脑城购买更优惠?
已知一次函数y1=-2x+1,y2=x-2.
⑴当x分别满足什么条件时,y1=y2,y1<y2,y1>y2?
⑵在同一直角坐标系中作出这两个函数的图象,并用自己的话归纳出⑴中的答案与函数图象之间的关系.
如图所示, ,
,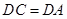 ,
,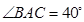 ,
,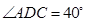 .
.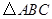 与
与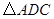 不可能全等,说明理由.
不可能全等,说明理由.
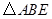 与
与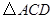 全等,
全等,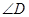 与
与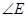 对应,顶点
对应,顶点 与
与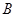 对应,写出其他对应角及对应顶点.
对应,写出其他对应角及对应顶点.
如图所示, ,
, ,
, ,
, ,
,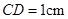 ,
,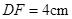 ,求:
,求: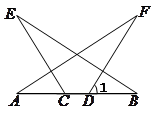
(1)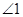 的度数;
的度数;
(2)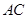 的长.
的长.