通常,我们把长方形和正方形统称为矩形.如图1,是一个长为2a,宽为2b的矩形ABCD,若把此矩形沿图中的虚线用剪刀均分为4块小长方形,然后按照图2的形状拼成一个正方形MNPQ.
(1)分别从整体和局部的角度出发,计算图2中阴影部分的面积,可以得到等式 _________ .
(2)仔细观察长方形ABCD与正方形MNPQ,可以发现它们的 _________ 相同, _________ 不同.(选填“周长”或“面积”)
(3)根据上述发现,猜想结论:用总长为36米的篱笆围成一个矩形养鸡场,可以有许多不同的围法.在你围的所有矩形中,面积最大的矩形的面积是 _________ 米2.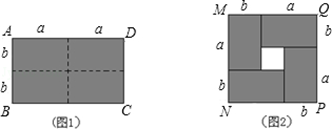
如图,在平面直角坐标系中, 与 轴的正半轴交于 、 两点,与 轴的正半轴相切于点 ,连接 、 ,已知 半径为2, ,双曲线 经过圆心 .
(1)求双曲线 的解析式;
(2)求直线 的解析式.

2018年高一新生开始,湖南全面启动高考综合改革,实行“ ”的高考选考方案.“3”是指语文、数学、外语三科必考;“1”是指从物理、历史两科中任选一科参加选考,“2”是指从政治、化学、地理、生物四科中任选两科参加选考
(1)“ ”的选考方案共有多少种?请直接写出所有可能的选法;(选法与顺序无关,例如:“物、政、化”与“物、化、政”属于同一种选法)
(2)高一学生小明和小杰将参加新高考,他们酷爱历史和生物,两人约定必选历史和生物.他们还需要从政治、化学、地理三科中选一科参考,若这三科被选中的机会均等,请用列表或画树状图的方法,求出他们恰好都选中政治的概率.
如图,将 沿着 边翻折,得到 ,且 .
(1)判断四边形 的形状,并说明理由;
(2)若 , ,求四边形 的面积.

每年5月份是心理健康宣传月,某中学开展以“关心他人,关爱自己”为主题的心理健康系列活动.为了解师生的心理健康状况,对全体2000名师生进行了心理测评,随机抽取20名师生的测评分数进行了以下数据的整理与分析:
①数据收集:抽取的20名师生测评分数如下
85,82,94,72,78,89,96,98,84,65,
73,54,83,76,70,85,83,63,92,90.
②数据整理:将收集的数据进行分组并评价等级:
|
分数 |
|
|
|
|
|
|
人数 |
5 |
|
5 |
2 |
1 |
|
等级 |
|
|
|
|
|
③数据分析:绘制成不完整的扇形统计图:
④依据统计信息回答问题
(1)统计表中的 .
(2)心理测评等级 等的师生人数所占扇形的圆心角度数为 .
(3)学校决定对 等的师生进行团队心理辅导,请你根据数据分析结果,估计有多少师生需要参加团队心理辅导?

我国于2019年6月5日首次完成运载火箭海上发射,这标志着我国火箭发射技术达到了一个崭新的高度.如图,运载火箭从海面发射站点 处垂直海面发射,当火箭到达点 处时,海岸边 处的雷达站测得点 到点 的距离为8千米,仰角为 .火箭继续直线上升到达点 处,此时海岸边 处的雷达测得 处的仰角增加 ,求此时火箭所在点 处与发射站点 处的距离.(结果精确到0.1千米)(参考数据: ,