如图1,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A开始以1cm/s的速度沿AB边向点B运动,点Q从点B以2cm/s的速度沿BC边向点C运动,如果P、Q同时出发,设运动时间为ts,
(1)当t=2时,求△PBQ的面积;
(2)当t= 时,试说明△DPQ是直角三角形;
时,试说明△DPQ是直角三角形;
(3)当运动3s时,P点停止运动,Q点以原速立即向B点返回,在返回的过程中,DP是否能平分∠ADQ?若能,求出点Q运动的时间;若不能,请说明理由.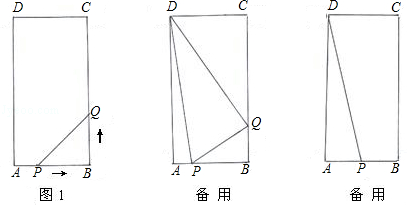
已知二次函数y=x2﹣4x+3.
(1)用配方法求其图象的顶点C的坐标,并描述该函数的函数值随自变量的增减而变化的情况;
(2)求函数图象与x轴的交点A,B的坐标,及△ABC的面积.
如图,在平面直角坐标系中,直线 与抛物线
与抛物线 交于A、B两点,点A在x轴上,点B的横坐标为-8.
交于A、B两点,点A在x轴上,点B的横坐标为-8.
(1)求该抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.
①设△PDE的周长为l,点P的横坐标为x,求l关于x的函数关系式,并求出l的最大值;
②连接PA,以PA为边作图示一侧的正方形APFG.随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在y轴上时,直接写出对应的点P的坐标.
定义:如图1,射线OP与原点为圆心,半径为1的圆交于点P,记∠xOP=α,则点P的横坐标叫做角 的余弦值,记作
的余弦值,记作 ;点P的纵坐标叫做角
;点P的纵坐标叫做角 的正弦值,记作
的正弦值,记作 ;纵坐标与横坐标的比值叫做角
;纵坐标与横坐标的比值叫做角 的正切值,记作
的正切值,记作 .
.
如:当 时,点P的横坐标为
时,点P的横坐标为 =
= ,纵坐标为
,纵坐标为 =
= 即P(
即P( ,
, ).
).
又如:在图2中, (
( 为锐角), PN
为锐角), PN
 轴,QM
轴,QM
 轴,易证△OQM≌△OPN, 则Q点的纵坐标
轴,易证△OQM≌△OPN, 则Q点的纵坐标 等于点P的横坐标
等于点P的横坐标 ,得
,得 =
=  .
.
解决以下四个问题:
(1)当 时,求点P的坐标;
时,求点P的坐标;
(2)当 是锐角时,则
是锐角时,则 +
+ 1(用>或<填空),
1(用>或<填空), = ;
= ;
(3)求证: (
( 为锐角);
为锐角);
(4)求证:tan =
= (
( 为锐角);
为锐角);
某学校开展“青少年科技创新比赛”活动,“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车同时分别从A,B出发,沿轨道到达C处,在AC上,甲的速度是乙的速度的1.5倍,设t后甲、乙两遥控车与B处的距离分别为 ,
, ,则
,则 ,
, 与t的函数关系如图,试根据图象解决下列问题:
与t的函数关系如图,试根据图象解决下列问题:
(1)填空:乙的速度 =米/分;
=米/分;
(2)写出 与t的函数关系式;
与t的函数关系式;
(3)若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰,试探求什么时间两遥控车的信号不会产生相互干扰?
如图,AB为的直径,点C在⊙O上,点P是直径AB上的一点(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q.
(1)在线段PQ上取一点D,使DQ=DC,连接DC,试判断CD与⊙O的位置关系,并说明理由.
(2)若cosB= ,BP=6,AP=1,求QC的长.
,BP=6,AP=1,求QC的长.