已知 为实数,
为实数,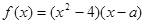
(1)求导数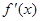 ;
;
(2)若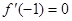 ,求
,求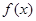 在[-2,2] 上的最大值和最小值;
在[-2,2] 上的最大值和最小值;
(3)若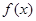 在
在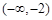 和
和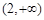 上都是递增的,求
上都是递增的,求 的取值范围.
的取值范围.
在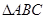 中,角
中,角 的对边分别为
的对边分别为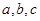 ,且
,且 成等差数列
成等差数列
(1)若 ,求
,求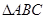 的面积
的面积
(2)若 成等比数列,试判断
成等比数列,试判断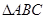 的形状
的形状
在平面直线坐标系XOY中,给定两点A(1,0),B(0,-2),点C满足 ,其中
,其中 ,且
,且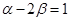 .
.
(1)求点C的轨迹方程.
(2)设点C的轨迹与双曲线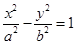 (
(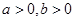 )相交于M,N两点,且以MN为直径的圆经过原点,求证:
)相交于M,N两点,且以MN为直径的圆经过原点,求证: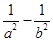 是定值.
是定值.
(3)在(2)条件下,若双曲线的离心率不大于 ,求该双曲线实轴的取值范围.
,求该双曲线实轴的取值范围.
已知数列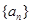 的前n项和为
的前n项和为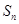 ,且满足
,且满足 各项为正数的数列
各项为正数的数列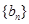 中,对一切
中,对一切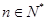 ,有
,有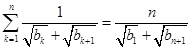 ,且
,且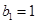 ,
, ,
,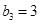 .
.
(1)求数列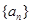 和
和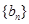 的通项公式.
的通项公式.
(2)设数列 的前n项和为
的前n项和为 ,求
,求 .
.
设函数
(1)若函数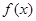 在
在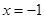 处取得极值-2,求a,b的值.
处取得极值-2,求a,b的值.
(2)若函数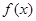 在区间(-1,1)内单调递增,求b的取值范围.
在区间(-1,1)内单调递增,求b的取值范围.
某省对省内养殖场“瘦肉精”使用情况进行检查,在全省的养殖场随机抽取M个养殖场的猪作为样本,得到M个养殖场“瘦肉精”检测阳性猪的头数,根据此数据作出了频率分布表和频率分布直方图如下: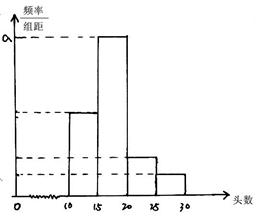
| 分组 |
频数 |
频率 |
 |
10 |
0.25 |
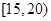 |
24 |
n |
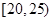 |
m |
P |
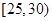 |
2 |
0.05 |
| 合计 |
M |
1 |
(1)求出表中M,P以及图中a的值.
(2)若该省有这样规模的养殖场240个,试估计该省“瘦肉精”检测呈阳性的猪的头数在区间 内的养殖场的个数.
内的养殖场的个数.
(3)在所取样本中,出现“瘦肉精”呈阳性猪的头数不少于20头的养殖场中任选2个,求至多一个养殖场出现“瘦肉精”阳性猪头数在区间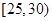 内的概率.
内的概率.