已知函数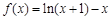 .
.
(1)求函数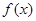 的单调递减区间;
的单调递减区间;
(2)若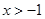 ,证明:
,证明: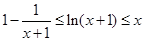 .
.
(本小题满分12分)
已知奇函数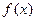 的定义域为
的定义域为 ,且在
,且在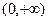 上为增函数,
上为增函数,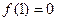 .
.
(1)求不等式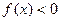 的解集;
的解集;
(2)设函数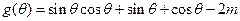 ,
,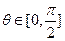 ,若不等式组
,若不等式组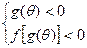 恒成立,
恒成立,
求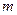 的取值范围.
的取值范围.
(本小题满分12分)
已知向量 ,
,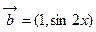 ,函数
,函数 .
.
(1)求函数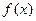 的最小正周期以及单调递增区间;
的最小正周期以及单调递增区间;
(2)若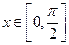 时, 求
时, 求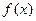 的值域;
的值域;
(3)求方程 在
在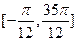 内的所有实数根之和.
内的所有实数根之和.
(本小题满分12分)
对甲、乙的学习成绩进行抽样分析,各抽 门功课,得到的观测值如下:
门功课,得到的观测值如下:
分别计算两个样本的平均数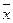 和方差
和方差 ,并根据计算结果估计甲、乙谁的平均成绩较好?谁的各门功课发展较平衡?
,并根据计算结果估计甲、乙谁的平均成绩较好?谁的各门功课发展较平衡?
(本小题满分12分)
某市地铁全线共有四个车站,甲、乙两人同时在地铁第一号车站(首发站)乘车.假设每人自第2号车站开始,在每个车站下车是等可能的。约定用有序实数对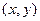 表示“甲在
表示“甲在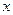 号车站下车,乙在
号车站下车,乙在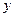 号车站下车”.
号车站下车”.
(1)用有序实数对把甲、乙两人下车的所有可能的结果列举出来;
(2)求甲、乙两人同在第3号车站下车的概率;
(3)求甲、乙两人在不同的车站下车的概率.
(本小题满分12分)
已知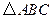 中,角
中,角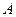 、
、 、
、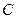 所对的边分别为
所对的边分别为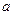 、
、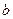 、
、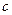 ,
,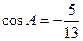 ,
,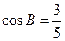 .
.
(1)求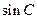 的值;
的值;
(2)若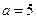 ,求
,求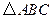 的面积.
的面积.