(本小题满分12分)
对甲、乙的学习成绩进行抽样分析,各抽 门功课,得到的观测值如下:
门功课,得到的观测值如下:
分别计算两个样本的平均数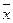 和方差
和方差 ,并根据计算结果估计甲、乙谁的平均成绩较好?谁的各门功课发展较平衡?
,并根据计算结果估计甲、乙谁的平均成绩较好?谁的各门功课发展较平衡?
已知 =(3,2),
=(3,2), =
= (-1,2),
(-1,2), =(4,1).(1)
=(4,1).(1) 求满足
求满足 =x
=x +y
+y 的实数x,y的值; (2)若(
的实数x,y的值; (2)若( +k
+k )
) (2
(2 -
- ),求实数k的值.
),求实数k的值.
已知函数
(1)当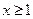 时, 证明: 不等式
时, 证明: 不等式 恒成立;
恒成立;
(2)若数列 满足
满足 ,证明数列
,证明数列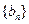 是等比数列,并求出数列
是等比数列,并求出数列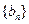 、
、 的通项公式;
的通项公式;
(3)在(2)的条件下,若 ,证明:
,证明: .
.
如图,椭圆的中心在原点, 为椭圆的左焦点,
为椭圆的左焦点, 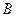 为椭圆的一个顶点,过点
为椭圆的一个顶点,过点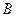 作与
作与 垂直的直线
垂直的直线 交
交 轴于
轴于 点, 且椭圆的长半轴长
点, 且椭圆的长半轴长 和短半轴长
和短半轴长 是关于
是关于 的方程
的方程 (其中
(其中 为半焦距)的两个根.
为半焦距)的两个根.
(1)求椭圆的离心率;
(2)经过 、
、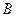 、
、 三点的圆与直线
三点的圆与直线 相切,试求椭圆的方程.
相切,试求椭圆的方程.
已知函数 (
( 为实常数).
为实常数).
(1)当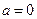 时,求
时,求 的最小值;
的最小值;
(2)若 在
在 上是单调函数,求
上是单调函数,求 的取值范围.
的取值范围.
已知四边形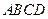 为矩形,
为矩形,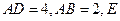 、
、 分别是线段
分别是线段 、
、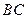 的中点,
的中点, 平面
平面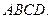 (1)求证:
(1)求证: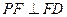 ;
;
(2)设点 在
在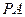 上,且
上,且 平面
平面 ,试确定点
,试确定点 的位置.
的位置.