若 是函数
是函数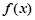 在点
在点 附近的某个局部范围内的最大(小)值,则称
附近的某个局部范围内的最大(小)值,则称 是函数
是函数 的一个极值,
的一个极值, 为极值点.已知
为极值点.已知 ,函数
,函数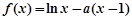 .
.
(Ⅰ)若 ,求函数
,求函数 的极值点;
的极值点;
(Ⅱ)若不等式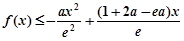 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(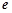 为自然对数的底数)
为自然对数的底数)
设
,集合
.
(1)求集合
(用区间表示);
(2)求函数
在
内的极值点.
在平面直角坐标系
中,已知椭圆
:
,
,且椭圆
上的点到点
的距离的最大值为
.
(1)求椭圆
的方程;
(2)在椭圆
上,是否存在点
,使得直线
:
与圆
:
相交于不同的两点
、
,且
的面积最大?若存在,求出点
的坐标及对应的
的面积;若不存在,请说明理由.
设数列
的前
项和为Sn,满足
,且
,
,
成等差数列.
(1)求
的值;
(2)求数列
的通项公式;
(3)证明:对一切正整数
,有
.
如图所示,在四棱锥
中,底面
为矩形,
平面
,点
在线段
上,
平面
.
(1)证明:
平面
;
(2)若
,
,求二面角
的正切值.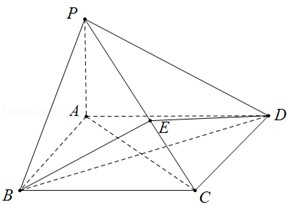
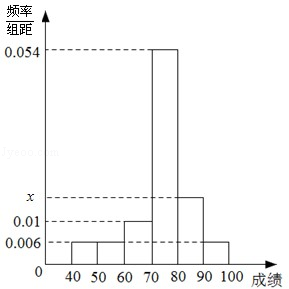
某班50位学生期中考试数学成绩的频率直方分布图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].
(1)求图中
的值;
(2)从成绩不低于80分的学生中随机选取2人,该2人中成绩在90分以上(含90分)的人数记为
,求
的数学期望.