如图,三角形ABC是以BC为底边的等腰三角形,点A、C分别是一次函数y=- x+3的图象与y轴、x轴的交点,点B在二次函数
x+3的图象与y轴、x轴的交点,点B在二次函数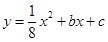 的图象上,且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形.
的图象上,且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形.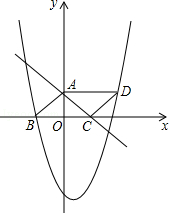
(1)试求b,c的值,并写出该二次函数表达式;
(2)动点P从A到D,同时动点Q从C到A都以每秒1个单位的速度运动,问:
①当P运动到何处时,有PQ⊥AC?
②当P运动到何处时,四边形PDCQ的面积最小?此时四边形PDCQ的面积是多少?
如图,已知AB是⊙O的直径,点C、D在⊙O上,过D点作PF∥AC交⊙O于F,交AB于点E,∠BPF=∠ADC.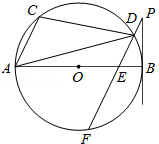
(1)求证:BP是⊙O的切线;
(2)求证:AE•EB=DE•EF;
(3)当⊙O的半径为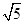 ,AC=2,BE=1时,求BP的长.
,AC=2,BE=1时,求BP的长.
如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y= 的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,-2),tan∠BOC=
的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,-2),tan∠BOC= .
.
(1)求该反比例函数和一次函数的解析式.
(2)求△BOC的面积.
(3)P是x轴上的点,且△PAC的面积与△BOC的面积相等,求P点的坐标.
准备两组相同的牌,每组三张大小一样,三张牌的牌面数字分别为-1,0,1.从每组中各模出一张牌.
(1)两张牌的牌面数字和等于1的概率是多?
(2)两张牌的牌面数字和等于几的概率最大?
(3)两张牌的牌面数字和大于0的概率是多少
儿童节期间,文具商店搞促销活动,同时购买一个书包和一个文具盒可以打8折优惠,能比标价省14元,已知书包标价比文具盒标价的3倍少6元,那么书包和文具盒的标价各是多少元.