如图,为测楼房BE的高,用测量仪在距楼底部30米的D处,用高1.2米的测角仪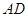 测得楼顶B的仰角α为60°.求楼房BE的高度.(精确到0.1米).
测得楼顶B的仰角α为60°.求楼房BE的高度.(精确到0.1米).
如图,在△ABC和△ACD中,CB=CD,设点E是CB的中点,点F是CD的中点.
(1)请你在图中作出点E和点F(尺规作图,保留作图痕迹,不写作法与证明);
(2)连接AE、AF,若∠ACB=∠ACD,请问△ACE≌△ACF吗?请说明理由.
先化简 ÷
÷ ,再选取一个既使原式有意
,再选取一个既使原式有意
义,又是你喜欢的数代入求值.
某储运站现有甲种货物1530吨,乙种货物1150吨,安排用一列货车将这批货物运往外地,这列货车持A、B两种类型的货厢共50节。已知甲种货物35吨和乙种货物15吨可装满一节A型货厢,甲种货物25吨和乙种货物35吨可装满一节B型货厢,问:该储运站需配置A、B两种类型的货厢各几节?
(12分)2011年2月,某网站作“认为我们国家今年的经济状况会怎么样?”的调查,结果显示:认为“经济保持平稳”占42.4%;认为“经济逐渐繁荣”占16.7%;认为“经济放缓或下行”占33.1%;回答“不清楚”的也占一部分。统计结果见下图。请根据上述内容解答下列问题:
(1)图中“经济逐渐繁荣”这一组的条形图画得不完整,请补全;
(2)回答“不清楚”的所占比例为_____________;
(3)回答“经济放缓或下行”的人数为0.662万,那么认为“经济逐渐繁荣”的人数是_________万人;
(4)认为“经济保持平稳”和“经济逐渐繁荣的被访者占到了近_________成(注:一成=10%)。
在2010年上海世博会期间,某超市在销售中发现:吉祥物—“海宝”
平均每天可售出20套,每件盈利40元。国庆长假商场决定采取适当的降价措施,扩大销售
量,增加盈利,尽快减少库存。经市场调查发现:如果每套降价4元,那么平均每天就可多
售出8套。要想平均每天在销售吉祥物上盈利1200元,那么每套应降价多少?