《愤怒的小鸟》是一款时下非常流行的游戏,故事也相当有趣,如图11甲所示,为了报复偷走鸟蛋的肥猪们,鸟儿以自己的身体为武器,如炮弹般弹射出去攻击肥猪们的堡垒.某班的同学们根据自己所学的物理知识进行假设:小鸟被弹弓沿水平方向弹出,如图乙所示.h1=0.8 m,l1=2 m,h2=2.4 m,l2=1 m (取重力加速度g=10 m/s2):
(1)肥猪A在台面草地的右边缘,若要击中A,小鸟的初速度为多大?
(2)小鸟弹出后能否直接打中地面草地上肥猪的堡垒?请列式计算进行说明。
(3)如果小鸟弹出后,先掉到台面的草地上,接触地面瞬间竖直速度变为零,水平速度不变,小鸟在草地上滑行一段距离后飞出,若要打中肥猪的堡垒,小鸟和草地间的动摩擦因数μ与小鸟弹出时的初速度v0应满足什么关系(用题中所给的符号h1、l1、h2、l2、g表示)?
从距离地面80 m的高空自由下落一个小球,若取g=10 m/s2,求小球落地前最后1 s内的位移.
如图所示,是某质点运动的v-t图象,请回答:
(1)在0~4s内、4~8s内、10~12s内质点加速度各是多少?
(2)质点在0~12s内的位移大小是多少?
如图所示,光滑水平面上A、B两小球沿同一方向运动,A球的动量为4kgm/s,B球的质量为1kg,速度为6m/s,已知两球相碰后,A球的动量减为原来的一半,方向与原方向一致。求:
(1)碰撞后B球的速度变为多大?
(2)A球的质量范围。
一列横波在x轴上传播,在t1 = 0时刻波形如图中实线所示,t2 = 0.05s时刻波形如图中虚线所示.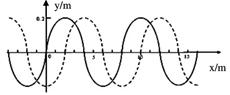
(1)求这列波的波速?
(2)若有另一列波能与这列波发生稳定干涉,则另一列波的最小频率是多少?
如图所示,矩形区域Ⅰ和Ⅱ内分别存在方向垂直于纸面向外和向里的匀强磁场(AA′、BB′、CC′、DD′为磁场边界,四者相互平行),磁感应强度大小均为B,矩形区域的长度足够长,两磁场宽度及BB′与CC′之间的距离均相同。某种带正电的粒子从AA′上的O1处以大小不同的速度沿与O1A成α=30°角进入磁场(如图所示,不计粒子所受重力),当粒子的速度小于某一值时,粒子在区域Ⅰ内的运动时间均为t0;当速度为v0时,粒子在区域Ⅰ内的运动时间为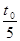 。求:
。求:
⑴粒子的比荷 ;
;
⑵磁场区域Ⅰ和Ⅱ的宽度d;
⑶速度为v0的粒子从O1到DD′所用的时间。