已知集合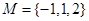 ,
, ,
, .从集合
.从集合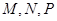 中各取一个元素分别记为
中各取一个元素分别记为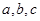 ,设方程
,设方程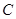 为
为 .
.
(1)求方程 表示焦点在
表示焦点在 轴上的双曲线的概率.
轴上的双曲线的概率.
(2)求方程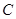 不表示椭圆也不表示双曲线的概率.
不表示椭圆也不表示双曲线的概率.
(本小题满分10分)
在某中学举行的物理知识竞赛中,将三个年级参赛学生的成绩再进行整理后分成5组,绘制出如图所示的频率分布直方图,图中从左到右依次为第一、第二、第三、第四、第五小组,已知第三小组的频数是15.
(1)求成绩在50-70分的频率是多少?
(2)求这三个年级参赛学生的总人数是多少?
(3)求成绩在80-100分的学生人数是多少?
(本小题满分8分)
一个学校的足球队、篮球队和排球队分别有28,22,17名成员,一些成员不止参加一支球队,具体情况如图所示,随机选取的一名成员:
(1)属于不止1支球队的概率是多少?
(2)属于不超过2支球队的概率是多少?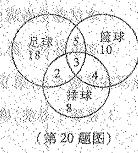
(本小题满分8分)
已知 都是锐角,
都是锐角,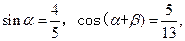
(Ⅰ)求 的值
的值
(Ⅱ)求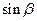 的值
的值
(本小题满分14分)已知函数f(x)=alnx+x2(a为实常数).
(Ⅰ)若a=-2,求证:函数f(x)在(1,+∞)上是增函数;
(Ⅱ)求函数f(x)在[1,e]上的最小值及相应的x值;
(本小题满分12分)假设关于某设备使用年限x(年)和所支出的维修费用y(万元)有如下统计资料:
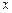 |
2 |
3 |
4 |
5 |
6 |
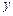 |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
若由资料知,y对x呈线性相关关系,试求:
(1)回归直线方程;
(2)估计使用年限为10年时,维修费用约是多少?