(本小题满分14分)设b>0，椭圆方程为
，抛物线方程为
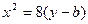.如图4所示,过点F(0,b+2)作x轴的平行线，与抛物线在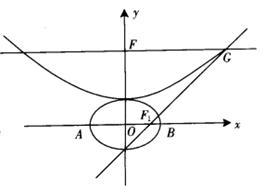
第一象限的交点为G.已知抛物线在点G的切线经
过椭圆的右焦点
.
(1)求满足条件的椭圆方程和抛物线方程;
(2)设A,B分别是椭圆长轴的左、右端点，试探究在
抛物线上是否存在点P，使得△ABP为直角三角形？
若存在，请指出共有几个这样的点？并说明理由
（不必具体求出这些点的坐标）.
六人按下列要求站一横排，分别有多少种不同的站法？
（l）甲不站两端；
（2）甲、乙必须相邻；
（3）甲、乙不相邻；
（4）甲、乙之间间隔两人；
（5）甲不站左端，乙不站右端．
（本小题满分14分）已知数列
的前
项和
，数列
的通项为
，且
满足：
①
；②对任意正整数
都有
成立．
（1）求
与
；
（2）设数列
的前项和为
，求证：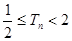
（
）；
（3）数列中是否存在三项，使得这三项按原有的顺序构成等差数列，若存在，求出这三项，若不存在，说明理由．
（本小题满分13分）已知向量
，
，函数
（1）求函数
的最小正周期及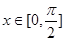
上的最值；
（2）若关于
的方程
在区间
上只有一个实根，求实数
的取值范围．
（本小题满分12分）马航
牵动全球人的心，世界各国积极投身到马航的搜救工作中，了解海底构造是救援工作要做的第一件事．某搜救队在某海域的海平面上的同一条直线上的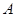
，
，
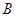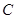三点进行测量，得
，
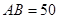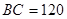，于，，三处测得水深分别为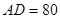
，
，
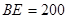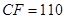，如图所示，试利用你所学知识求
的余弦值．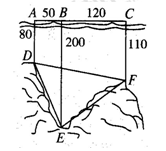
（本小题满分12分）已知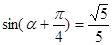
，
，
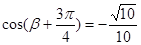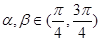，求
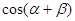的值．