如图,已知矩形ABCD中, ,
,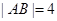 .将矩形ABCD沿对角线BD折起,使得面BCD⊥面ABD.现以D为原点,DB作为y轴的正方向,建立如图空间直角坐标系,此时点A恰好在xDy坐标平面内.试求A,C两点的坐标.
.将矩形ABCD沿对角线BD折起,使得面BCD⊥面ABD.现以D为原点,DB作为y轴的正方向,建立如图空间直角坐标系,此时点A恰好在xDy坐标平面内.试求A,C两点的坐标.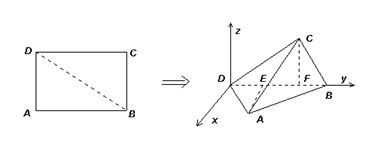
如图,在四棱锥P-ABCD中,底面ABCD为正方形,且边长为2a,棱PD⊥底面ABCD,PD=2b,取各侧棱的中点E,F,G,H,写出点E,F,G,H的坐标.
如图,长方体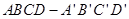 中,
中,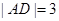 ,
,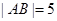 ,
, ,设E为
,设E为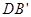 的中点,F为
的中点,F为 的中点,在给定的空间直角坐标系D-xyz下,试写出A,B,C,D,
的中点,在给定的空间直角坐标系D-xyz下,试写出A,B,C,D, ,
,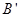 ,
,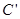 ,
, ,E,F各点的坐标.
,E,F各点的坐标.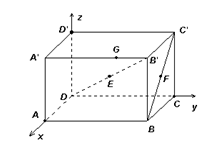
求圆心在直线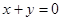 上,且过两圆
上,且过两圆 ,
,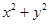
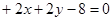 交点的圆的方程.
交点的圆的方程.
已知圆 和直线
和直线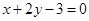 交于P、Q两点,且OP⊥OQ(O为坐标原点),求该圆的圆心坐标及半径长.
交于P、Q两点,且OP⊥OQ(O为坐标原点),求该圆的圆心坐标及半径长.