已知关于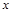 的方程
的方程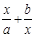 =1,其中
=1,其中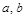 为实数.
为实数.
(1)若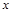 =1-
=1-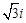 是该方程的根,求
是该方程的根,求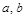 的值.
的值.
(2)当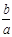 >
>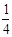 且
且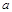 >0时,证明该方程没有实数根.
>0时,证明该方程没有实数根.
经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元。根据历史资料,得到销售季度内市场需求量的频率分布直方图,如右图所示。经销商为下一个销售季度购进了130t该农产品。以x(单位:t,100≤x≤150)表示下一个销售季度内经销该农产品的数量,T表示利润.
(1)将T表示为x的函数
(2)根据直方图估计利润T不少于57000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若x ,则取x=105,且x=105的概率等于需求量落入[100,110
,则取x=105,且x=105的概率等于需求量落入[100,110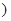 ,求T的数学期望.
,求T的数学期望.
设袋子中装有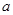 个红球,
个红球,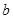 个黄球,
个黄球,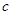 个蓝球,且规定:取出一个红球得1分,
个蓝球,且规定:取出一个红球得1分,
取出一个黄球2分,取出蓝球得3分。
(1)当 时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量
时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量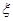 为取出此2球所得分数之和,.求
为取出此2球所得分数之和,.求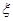 分布列;
分布列;
(2)从该袋子中任取(且每球取到的机会均等)1个球,记随机变量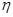 为取出此球所得分数.若
为取出此球所得分数.若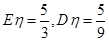 ,求
,求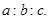
一个盒子里装有7张卡片, 其中有红色卡片4张, 编号分别为1, 2, 3, 4; 白色卡片3张, 编号分别为2, 3, 4.从盒子中任取4张卡片 (假设取到任何一张卡片的可能性相同).
(1)求取出的4张卡片中, 含有编号为3的卡片的概率.
(2)再取出的4张卡片中, 红色卡片编号的最大值设为X, 求随机变量X的分布列和数学期望.
在一场娱乐晚会上, 有5位民间歌手(1至5号)登台演唱, 由现场数百名观众投票选出最受欢迎歌手.各位观众须彼此独立地在选票上选3名选手, 其中观众甲是1号歌手的歌迷, 他必选1号, 不选2号, 另在3至5号中随机选2名.观众乙和丙对5位歌手的演唱没有偏爱, 因此在1至5号中随机选3名歌手.
(1)求观众甲选中3号歌手且观众乙未选中3号歌手的概率;
(2)X表示3号歌手得到观众甲、乙、丙的票数之和, 求X的分布列和数学期望.
某高校数学系计划在周六和周日各举行一次主题不同的心理测试活动,分别由李老师和张老师负责,已知该系共有 位学生,每次活动均需该系
位学生,每次活动均需该系 位学生参加(
位学生参加( 和
和 都是固定的正整数)。假设李老师和张老师分别将各自活动通知的信息独立、随机地发给该系
都是固定的正整数)。假设李老师和张老师分别将各自活动通知的信息独立、随机地发给该系 位学生,且所发信息都能收到。记该系收到李老师或张老师所发活动通知信息的学生人数为
位学生,且所发信息都能收到。记该系收到李老师或张老师所发活动通知信息的学生人数为
(1)求该系学生甲收到李老师或张老师所发活动通知信息的概率;
(2)求使 取得最大值的整数
取得最大值的整数 。
。