如图,已知一四棱锥P-ABCD的底面是边长为1的正方形,且侧棱PC⊥底面ABCD,且PC=2,E是侧棱PC上的动点
(1)求四棱锥P-ABCD的体积;
(2)证明:BD⊥AE。
(本小题满分14分)
已知函数 (
(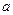 >0)的图象在点
>0)的图象在点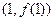 处的切线方程为
处的切线方程为 .
.
(Ⅰ)用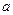 表示
表示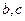 ;
;
(Ⅱ)若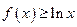 在
在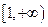 上恒成立,求
上恒成立,求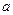 的取值范围;
的取值范围;
(Ⅲ)证明:1+ +
+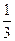 +…+
+…+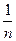 >
>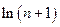 +
+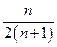
 .
.
(本小题满分14分)
在平面直角坐标系 中,设点
中,设点 (1,0),直线
(1,0),直线 :
: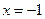 ,点
,点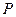 在直线
在直线 上移动,
上移动, 是线段
是线段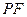 与
与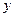 轴的交点,
轴的交点, 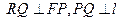 .
.
(Ⅰ)求动点 的轨迹方程;
的轨迹方程;
(Ⅱ) 记 的轨迹方程为
的轨迹方程为 ,过点
,过点 作两条互相垂直的曲线
作两条互相垂直的曲线 的弦
的弦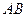 、
、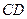 ,设
,设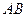 、
、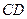 的中点分别为
的中点分别为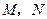 .求证:直线
.求证:直线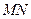 必过定点
必过定点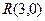 .
.
(本小题满分14分)
按照某学者的理论,假设一个人生产某产品单件成本为 元,如果他卖出该产品的单价为
元,如果他卖出该产品的单价为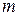 元,则他的满意度为
元,则他的满意度为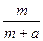 ;如果他买进该产品的单价为
;如果他买进该产品的单价为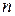 元,则他的满意度为
元,则他的满意度为 .如果一个人对两种交易(卖出或买进)的满意度分别为
.如果一个人对两种交易(卖出或买进)的满意度分别为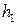 和
和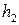 ,则他对这两种交易的综合满意度为
,则他对这两种交易的综合满意度为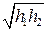 .
.
现假设甲生产A、B两种产品的单件成本分别为12元和5元,乙生产A、B两种产品的单件成本分别为3元和20元,设产品A、B的单价分别为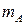 元和
元和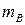 元,甲买进A与卖出B的综合满意度为
元,甲买进A与卖出B的综合满意度为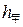 ,乙卖出A与买进B的综合满意度为
,乙卖出A与买进B的综合满意度为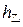 .
.
(1)求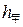 和
和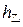 关于
关于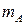 、
、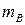 的表达式;当
的表达式;当 时,求证:
时,求证: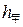 =
=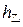 ;
;
(2)设 ,当
,当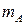 、
、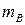 分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?
分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?
(本小题满分14分)
|


 如图,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面
如图,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面
|

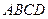 所成的角为45°,底面ABCD为直角梯形,
所成的角为45°,底面ABCD为直角梯形,
|



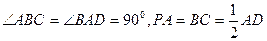
|
|
 (Ⅰ)求证:平面
(Ⅰ)求证:平面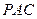 ⊥平面
⊥平面 ;
;
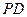 上是否存在一点
上是否存在一点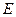 ,使
,使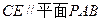 ?若存在,请确定E点的位置;若不存在,请说明理由.
?若存在,请确定E点的位置;若不存在,请说明理由.
(本小题满分12分)
在一次抗洪抢险中,准备用射击的方法引爆从桥上游漂流而下的一巨大汽油罐.已知只有5发子弹备用,且首次命中只能使汽油流出,再次命中才能引爆成功,每次射击命中率都是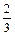 ,每次命中与否互相独立.
,每次命中与否互相独立.
(1) 求油罐被引爆的概率.
(2) 如果引爆或子弹打光则停止射击,设射击次数为ξ,求ξ的分布列及ξ的数学期望。