设函数
 ,其中
,其中 ,
, 为正整数,
为正整数, ,
, ,
, 均为常数,曲线
均为常数,曲线 在
在 处的切线方程为
处的切线方程为 .
.
(1)求 ,
, ,
, 的值;
的值;
(2)求函数 的最大值;
的最大值;
(3)证明:对任意的 都有
都有 .(
.( 为自然对数的底)
为自然对数的底)
已知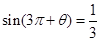 ,求
,求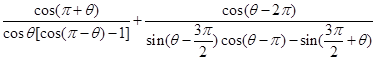 的值
的值
如图:内接于⊙O的△ABC的两条高线AD、BE相交于点H,过圆心O作OF⊥BC于 F,连接AF交OH于点G,并延长CO交圆于点I.
(1) 若 ,试求
,试求 的值;
的值;
(2)若 ,试求
,试求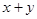 的值;
的值;
(3)若O为原点,点B的坐标为(-4,-3),点C的坐标为C(4,-3),试求点G的轨迹方程.
设
 .
.
(1)若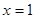 是函数
是函数 的极大值点,求
的极大值点,求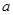 的取值范围;
的取值范围;
(2)当 时,若在
时,若在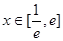 上至少存在一点
上至少存在一点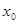 ,使
,使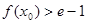 成立,求
成立,求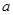 的取值范围.
的取值范围.
如图示,在四棱锥A-BHCD中,AH⊥面BHCD,此棱锥的三视图如下:
(1)求二面角B-AC-D的余弦弦值;
(2)在线段AC上是否存在一点E,使ED与面BCD成45°角?若存在,确定E的位置;若不存在,说明理由。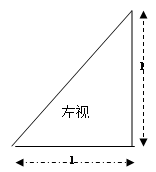

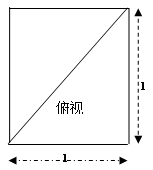
某市粮食储备库的设计容量为30万吨,年初库存粮食10万吨,从1月份起,计划每月收购粮食M万吨,每月供给市面粉厂粮食1万吨,另外每月还有大量的粮食外调任务。已知n个月内外调粮食的总量为 万吨与n的函数关系为
万吨与n的函数关系为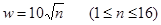 .要使在16个月内每月粮食收购之后能满足内、外调需要,且每月粮食调出后粮库内有不超过设计容量的储备粮,求M的范围。
.要使在16个月内每月粮食收购之后能满足内、外调需要,且每月粮食调出后粮库内有不超过设计容量的储备粮,求M的范围。