定义:若数列 对任意
对任意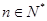 ,满足
,满足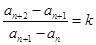 (
(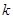 为常数),称数列
为常数),称数列 为等差比数列.
为等差比数列.
(1)若数列 前
前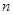 项和
项和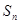 满足
满足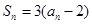 ,求
,求 的通项公式,并判断该数列是否为等差比数列;
的通项公式,并判断该数列是否为等差比数列;
(2)若数列 为等差数列,试判断
为等差数列,试判断 是否一定为等差比数列,并说明理由;
是否一定为等差比数列,并说明理由;
(3)若数列 为等差比数列,定义中常数
为等差比数列,定义中常数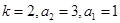 ,数列
,数列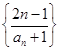 的前
的前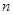 项和为
项和为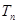 , 求证:
, 求证: .
.
.(本小题满分12分)
为了调查某中学高三学生的身高情况,在该中学高三学生中随机抽取了40名同学作为样本,测得他们的身高后,画出频率分布直方图如下: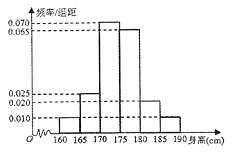
(I)估计该校高三学生的平均身高;
(II)从身高在180cm(含180cm)以上的样本中随机抽取2人,记身高在185~190cm之间的人数为X,求X的分布列和数学期望。
(本小题满分12分)
如图,正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD,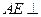 平面CDE
平面CDE
(I)求证: 平面ADE;
平面ADE;
(II)在线段BE上存在点M,使得直线M与平面EAD所成角的正弦值为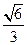 ,试确定点M的位置。
,试确定点M的位置。
.(本小题满分12分)
已知在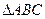 中,a,b,c分别是角A,B,C所对的边,且满足
中,a,b,c分别是角A,B,C所对的边,且满足
(I)求角A的大小;
(II)若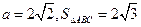 ,求b,c的长。
,求b,c的长。
(本小题满分12分)
已知数列 满足
满足
(I)求 的取值范围;
的取值范围;
(II)是否存在 ,使得
,使得 ?证明你的结论。
?证明你的结论。
(本小题 满分12分)
满分12分)
如图,双曲线 与抛物线
与抛物线 相交于
相交于
 ,直线AC、BD的交点为P(0,p)。
,直线AC、BD的交点为P(0,p)。
(I)试用m表示
(II)当m变化时,求p的取值范围。