在某社区举办的《有奖知识问答比赛》中，甲、乙、丙三人同时回答某一道题，已知甲回答对这道题的概率是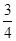
，甲、丙二人都回答错的概率是
，乙、丙二人都回答对的概率是
．
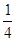（Ⅰ）求乙、丙二人各自回答对这道题的概率；
（Ⅱ）设乙、丙二人中回答对该题的人数为X，求X的分布列和数学期望．
已知函数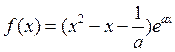
（
）
(Ⅰ) 当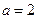
时,求函数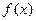
的单调区间;
(Ⅱ) 若不等式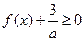
对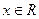
恒成立,求a的取值范围
已知棱长为1的正方体AC1，E、F分别是B1C1、C1D的中点．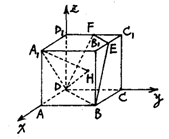
（1）求证：E、F、D、B共面；
（2）求点A1到平面的BDEF的距离；
（3）求直线A1D与平面BDEF所成的角．
如图5：正方体ABCD-A1B1C1D1，过线段BD1上一点P（P
平面ACB1）作垂直于D1B的平面分别交过D1的三条棱于E、F、G．
(1)求证：平面EFG∥平面A CB1，并判断三角形类型；
(2)若正方体棱长为a，求△EFG的最大面积，并求此时EF与B1C的距离．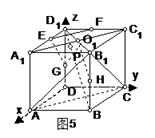
已知正方体ABCD－A1B1C1D1的棱长为2，点E为棱AB的中点，求：
（Ⅰ）D1E与平面BC1D所成角的大小；
（Ⅱ）二面角D－BC1－C的大小；
（Ⅲ）异面直线B1D1与BC1之间的距离．
在四棱锥P—ABCD中，底面ABCD是一直角梯形，∠BAD=90°，AD∥BC，AB=BC=a，AD=2a，且PA⊥底面ABCD，PD与底面成30°角．
（1）若AE⊥PD，E为垂足，求证：BE⊥PD；
（2）求异面直线AE与CD所成角的余弦值．