在某服装批发市场,某种品牌的时装当季节将来临时,价格呈上升趋势,设这种时装开始时定价为20元,并且每周(7天)涨价2元,从第6周开始保持30元的价格平稳销售;从第12周开始,当季节即将过去时,平均每周减价2元,直到第16周周末,该服装不再销售。
⑴试建立销售价y与周次x之间的函数关系式;
⑵若这种时装每件进价Z与周次 次之间的关系为Z=
次之间的关系为Z=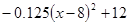 ,1≤
,1≤ ≤16,且
≤16,且 为整数,试问该服装第几周出售时,每件销售利润最大?最大利润为多少?
为整数,试问该服装第几周出售时,每件销售利润最大?最大利润为多少?
(本小题14分)
已知函 数
数
 .
.
(Ⅰ)若 ,求曲线
,求曲线 在
在 处切线的斜率;
处切线的斜率;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)设 ,若对任意
,若对任意 ,均存在
,均存在 ,使得
,使得 ,求
,求 的取值范围。
的取值范围。
((本小题12分)已知函数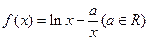 。
。
(1)判断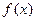 在定义域上的单调性;
在定义域上的单调性;
(2)若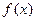 在
在 上的最小值为2,求
上的最小值为2,求 的值。
的值。
((本小题12分)某造船公司年造船量是20艘,已知造船 艘的产值函数为
艘的产值函数为 (单位:万元),成本函数为
(单位:万元),成本函数为 (单位:万元),又在经济学中,函数
(单位:万元),又在经济学中,函数 的边际函数
的边际函数 定义为
定义为 。
。
(Ⅰ)求利润函数 及边际利润函数
及边际利润函数 ;(提示:利润=产值-成本)
;(提示:利润=产值-成本)
(Ⅱ)问年造船量安排多少艘时,可使公司造船的年利润最大?
(Ⅲ)求边际利润函数 单调递减时
单调递减时 的取值范围。
的取值范围。

(本小题12分)
已知如下等式: ,
, ,
,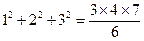 ,
,
当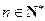 时,试猜想
时,试猜想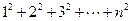 的值,并用数学归纳法给予证明。
的值,并用数学归纳法给予证明。