某市一公交线路某区间内共设置六个公交站点(如图所示),分别为 ,现在甲、乙两人同时从
,现在甲、乙两人同时从 站上车,且他们中的每个人在站点
站上车,且他们中的每个人在站点 下车是等可能。
下车是等可能。
求(1)甲在 或
或 站点下车的概率
站点下车的概率
(2)甲、乙两人不在同一站点下车的概率
(本小题满分15分) 已知函数 (其中
(其中 为锐角三角形的内角)且满足
为锐角三角形的内角)且满足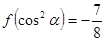 .
.
(1)求 的值;
的值;
(2)若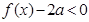 恒成立,求
恒成立,求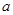 的取值范围.
的取值范围.
(本小题满分14分)设p:实数x满足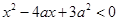 ,其中
,其中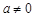 ,
,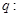 实数
实数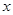
满足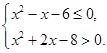
(Ⅰ)若
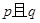 为真,求实数
为真,求实数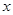 的取值范围;
的取值范围;
(Ⅱ)若p是q的必要不充分条件,求实数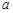 的取值范围.
的取值范围.
(本小题满分14分) △ABC中,a,b,c分别为内角A,B,C所对的边长,a= ,b=
,b=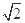 ,
,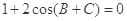 ,求边BC上的高.
,求边BC上的高.
在平面直角坐标系 中,已知圆
中,已知圆 和圆
和圆 .
.
(1)若直线 过点
过点 ,且被圆
,且被圆 截得的弦长为
截得的弦长为 ,求直线
,求直线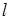 的方程;
的方程;
(2)在平面内是否存在一点 ,使得过点
,使得过点 有无穷多对互相垂直的直线
有无穷多对互相垂直的直线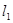 和
和 ,它们分别与圆
,它们分别与圆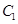 和圆
和圆 相交,且直线
相交,且直线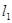 被圆
被圆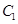 截得的弦长的
截得的弦长的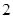 倍与直线
倍与直线 被圆
被圆 截得的弦长相等?若存在,求出所有满足条件的
截得的弦长相等?若存在,求出所有满足条件的 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表
| 商店名称 |
A |
B |
C |
D |
E E |
| 销售额(x)/千万元 |
3 |
5 |
6 |
7 |
9 9 |
| 利润额(y)/百万元 |
2 |
3 |
3 |
4 |
5 |
(1)画出销售额和利润额的散点图.(2)若销售额和利润额具有相关关系,用最小二乘法计算利润额y对销售额x的回归直线方程.