已知函数 .
.
(1)求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)直线 为曲线
为曲线 的切线,且经过原点,求直线
的切线,且经过原点,求直线 的方程及切点坐标.
的方程及切点坐标.
已知四棱柱 的底面是边长为1的正方形,侧棱垂直底边ABCD四棱柱,
的底面是边长为1的正方形,侧棱垂直底边ABCD四棱柱, ,
,
E是侧棱AA1的中点,求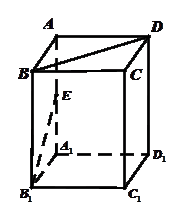
(1)求异面直线 与B1E所成角的大小;
与B1E所成角的大小;
(2)求四面体 的体积.
的体积.
已知双曲线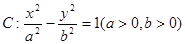 的两个焦点为
的两个焦点为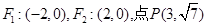 的曲线C上.(Ⅰ)求双曲线C的方程;
的曲线C上.(Ⅰ)求双曲线C的方程;
(Ⅱ)记O为坐标原点,过点Q (0,2)的直线l与双曲线C相交于不同的两点E、F,若△OEF的面积为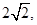 求直线l的方程
求直线l的方程
直线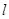 与椭圆
与椭圆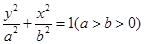 交于
交于 ,
, 两点,已知
两点,已知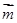
 ,
,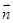
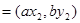 ,若
,若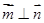 且椭圆的离心率
且椭圆的离心率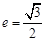 ,又椭圆经过点
,又椭圆经过点 ,
, 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线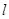 过椭圆的焦点
过椭圆的焦点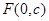 (
( 为半焦距),求直线
为半焦距),求直线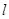 的斜率
的斜率 的值;
的值;
在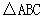 中,内角A,B,C所对的分别是a, b,c。已知a=2.c=
中,内角A,B,C所对的分别是a, b,c。已知a=2.c= ,
,  A=
A= .
.
(I)求sin C和b的值;
(II)求  (2A+
(2A+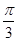 )的值.
)的值.
设数列 的前
的前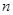 项和
项和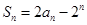 。
。
(1)求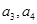 ;
;
(2)证明: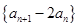 是等比数列;
是等比数列;