在3×3的方格纸中，点A、B、C、D、E、F分别位于如图所示-优题课

如图， $BD$ 为 $▱ ABCD$ 的对角线．

（1）作对角线 $BD$ 的垂直平分线，分别交 $AD$ ， $BC$ ， $BD$ 于点 $E$ ， $F$ ， $O$ （尺规作图，不写作法，保留作图痕迹）；

（2）连接 $BE$ ， $DF$ ，求证：四边形 $BEDF$ 为菱形．

为庆祝中国共产党建党100周年，某校举行了“红色华诞，党旗飘扬”党史知识竞赛．为了解竞赛成绩，抽样调查了七、八年级部分学生的分数，过程如下：

（1）收集数据．

从该校七、八年级学生中各随机抽取20名学生的分数，其中八年级的分数如下：

81 83 84 85 86 87 87 88 89 90

92 92 93 95 95 95 99 99 100 100

（2）整理、描述数据．

按下表分段整理描述样本数据：

分数 $x$

人数

年级

$80 ⩽ x < 85$

$85 ⩽ x < 90$

$90 ⩽ x < 95$

$95 ⩽ x ⩽ 100$

七年级

4

6

2

8

八年级

3

$a$

4

7

（3）分析数据．

两组样本数据的平均数中位数、众数、方差如表所示：

年级	平均数	中位数	众数	方差
七年级	91	89	97	40.9
八年级	91	$b$	$c$	33.2

根据以上提供的信息，解答下列问题：

①填空： $a =$ 　　， $b =$ 　　， $c =$ 　　；

②样本数据中，七年级甲同学和八年级乙同学的分数都为90分，　　同学的分数在本年级抽取的分数中从高到低排序更靠前（填“甲”或“乙” $)$ ；

③从样本数据分析来看，分数较整齐的是　　年级（填“七”或“八” $)$ ；

④如果七年级共有400人参赛，则该年级约有　　人的分数不低于95分．

如图，建筑物 $BC$ 上有一旗杆 $AB$ ，从与 $BC$ 相距 $20 m$ 的 $D$ 处观测旗杆顶部 $A$ 的仰角为 $52 °$ ，观测旗杆底部 $B$ 的仰角为 $45 °$ ，求旗杆 $AB$ 的高度（结果保留小数点后一位．参考数据： $\sin 52 ° \approx 0.79$ ， $\cos 52 ° \approx 0.62$ ， $\tan 52 ° \approx 1.28$ ， $\sqrt{2} \approx 1.41)$ ．

抛物线 $y = x^{2} - 1$ 交 $x$ 轴于 $A$ ， $B$ 两点 $(A$ 在 $B$ 的左边）．

（1） $▱ ACDE$ 的顶点 $C$ 在 $y$ 轴的正半轴上，顶点 $E$ 在 $y$ 轴右侧的抛物线上；

①如图（1），若点 $C$ 的坐标是 $(0, 3)$ ，点 $E$ 的横坐标是 $\frac{3}{2}$ ，直接写出点 $A$ ， $D$ 的坐标．

②如图（2），若点 $D$ 在抛物线上，且 $▱ ACDE$ 的面积是12，求点 $E$ 的坐标．

（2）如图（3）， $F$ 是原点 $O$ 关于抛物线顶点的对称点，不平行 $y$ 轴的直线 $l$ 分别交线段 $AF$ ， $BF$ （不含端点）于 $G$ ， $H$ 两点．若直线 $l$ 与抛物线只有一个公共点，求证： $FG + FH$ 的值是定值．

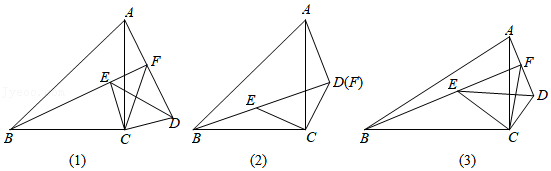
问题提出

如图（1），在 $ΔA BC$ 和 $ΔDEC$ 中， $∠ ACB = ∠ DCE = 90 °$ ， $BC = AC$ ， $EC = DC$ ，点 $E$ 在 $ΔABC$ 内部，直线 $AD$ 与 $BE$ 于点 $F$ ．线段 $AF$ ， $BF$ ， $CF$ 之间存在怎样的数量关系？

问题探究

（1）先将问题特殊化如图（2），当点 $D$ ， $F$ 重合时，直接写出一个等式，表示 $AF$ ， $BF$ ， $CF$ 之间的数量关系；

（2）再探究一般情形如图（1），当点 $D$ ， $F$ 不重合时，证明（1）中的结论仍然成立．

问题拓展

如图（3），在 $ΔABC$ 和 $ΔDEC$ 中， $∠ ACB = ∠ DCE = 90 °$ ， $BC = kAC$ ， $EC = kDC (k$ 是常数），点 $E$ 在 $ΔABC$ 内部，直线 $AD$ 与 $BE$ 交于点 $F$ ．直接写出一个等式，表示线段 $AF$ ， $BF$ ， $CF$ 之间的数量关系．