某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是: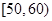 ,
,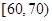 ,
, ,
,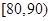 ,
,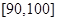 .
.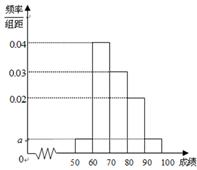
(1)求图中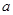 的值;
的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数(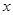 )与数学成绩相应分数段的人数(
)与数学成绩相应分数段的人数(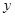 )之比如下表所示,求数学成绩在
)之比如下表所示,求数学成绩在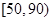 之外的人数.
之外的人数.
| 分数段 |
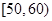 |
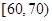 |
 |
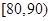 |
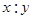 |
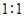 |
 |
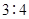 |
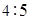 |
数列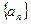 的各项均为正值,
的各项均为正值,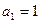 ,对任意
,对任意 ,
,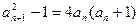 ,
,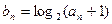 都成立.
都成立.
求数列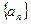 、
、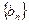 的通项公式;
的通项公式;
当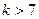 且
且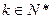 时,证明对任意
时,证明对任意 都有
都有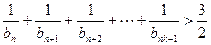 成立.
成立.
.设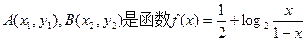 的图象上任意两点,且
的图象上任意两点,且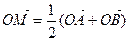 ,已知点M的横坐标为
,已知点M的横坐标为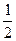 .
.
(I)求证:M点的纵坐标为定值;
(Ⅱ)若 ;
;
(Ⅲ)已知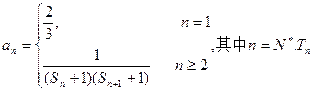 为数列
为数列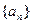 的前n项和,若
的前n项和,若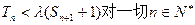 都成立,试求
都成立,试求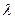 的取值范围.
的取值范围.
设 =
=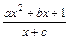 (a>0)为奇函数,且
(a>0)为奇函数,且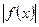 min=
min=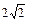 ,数列{an}与{bn}满足 如下关系:a1=2,
,数列{an}与{bn}满足 如下关系:a1=2,  ,
,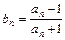 .
.
(1)求f(x)的解析表达式;
(2) 证明:当n∈N+时, 有bn
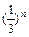 .
.
如图所示,动圆与定圆B:x2+y2-4y-32=0内切且过定圆内的一个定点A(0,-2),求动圆圆心P的轨迹方程.
如图,线段AB的两个端点A、B分别在x轴、y轴上滑动,|AB|=8,点M是AB上一点,且|AM|=3,点M随线段AB的运动而变化,求点M的轨迹.