设函数 ,集合
,集合 .
.
(1)若 ,求
,求 解析式。
解析式。
(2)若 ,且
,且 在
在 时的最小值为
时的最小值为 ,求实数
,求实数 的值。
的值。
已知椭圆的中心在原点,焦点在x 轴上,离心率为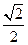 ,且椭圆经过圆C:
,且椭圆经过圆C: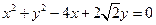 的圆心C。
的圆心C。
(1)求椭圆的方程;
(2)设直线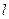 过椭圆的焦点且与圆C相切,求直线
过椭圆的焦点且与圆C相切,求直线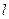 的方程。
的方程。
如图,在梯形ABCD中,AB∥CD,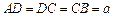 ,
,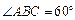 ,平面
,平面 平面
平面 ,四边形
,四边形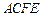 是矩形,
是矩形,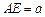 ,点
,点 在线段
在线段 上。
上。
(1)求证: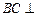 平面
平面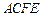 ;
;
(2)当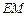 为何值时,
为何值时,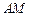 ∥平面
∥平面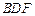 ?写出结论,并加以证明;
?写出结论,并加以证明;
(3)当EM为何值时,AM⊥BE?写出结论,并加以证明。
求与向量 =
=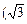 ,-1)和
,-1)和 =(1,
=(1, )夹角相等,且模为
)夹角相等,且模为 的向量
的向量 的坐标。
的坐标。
已知△ABC中,A(2,-1),B(3,2),C(-3,-1),BC边上的高为AD,求点D和向量 坐标。
坐标。
已知长方形ABCD,AB=3,BC=2,E为BC中点,P为AB上一点
(1)利用向量知识判定点P在什么位置时,∠PED=450;
(2)若∠PED=450,求证:P、D、C、E四点共圆。