设函数
.
（Ⅰ）判断
能否为函数
的极值点，并说明理由；
（Ⅱ）若存在
，使得定义在
上的函数
在处取得最大值，求实数
的最大值.
某商场有奖销售中，购满100元商品得1张奖券，多购多得。每1000张奖券为一个开奖单位，其中含特等奖1个，一等奖10个，二等奖50个。设1张奖券中特等奖、一等奖、二等奖的事件分别为A、B、C，求：
（1）P（A），P（B），P（C）；
（2）1张奖券的中奖概率；
（3）1张奖券不中特等奖且不中一等奖的概率。
已知c＞0，设命题p：函数y＝cx为减函数.命题q：当x∈[
，2]时，函数f(x)＝x＋
＞
恒成立.如果p或q为真命题，p且q为假命题.求c的取值范围.
已知A＝{x|x2≥9}，B＝{x|
≤0}，C＝{x||x－2|＜4}．
(1)求A∩B及A∪C；
(2)若U＝R，求A∩∁U(B∩C)
已知函数
①当
时，求曲线
在点
处的切线方程。
②求
的单调区间
已知函数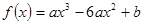
，问是否存在实数
使
在
上取最大值3，最小值-29，若存在，求出的值；不存在说明理由。