已知双曲线的中心在原点,焦点F1,F2在坐标轴上,离心率为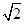 ,且过点(4,-
,且过点(4,-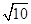 ).
).
(1)求双曲线方程;
(2)若点M(3,m)在双曲线上,求证: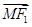 ·
·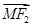 =0;
=0;
(3)求△F1MF2的面积.
棱长都相等的三棱锥的四个顶点都在同一外球面上,棱长为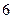 ;
;
(Ⅰ) 求此三棱锥的表面积;
(Ⅱ) 求此三棱锥的高;
(Ⅲ) 求此球的半径.
如图,在三棱锥,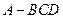 ,
,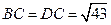 ,
,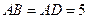 ,
,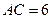 ,
,
(Ⅰ)求证: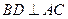 ;
;
(Ⅱ)求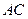 底面
底面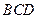 所成角
所成角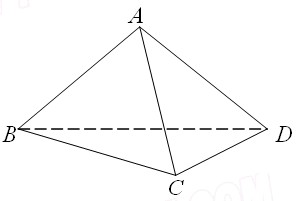
已知直线 :
: ,
, ,
, ,
,
(Ⅰ)求 与
与 交点
交点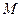 的坐标;
的坐标;
(Ⅱ)求过点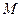 ,且与
,且与 垂直的直线方程.
垂直的直线方程.
如图,一个几何体的三视图△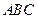 是边长为
是边长为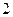 的等边三角形,
的等边三角形,
(Ⅰ)画出直观图;
(Ⅱ)求这个几何体的体积
(本小题满分14分)已知f (x)=mx(m为常数,m>0且m≠1).设f (a1),f (a2),…,f (an),…(n∈N)是首项为m2,公比为m的等比数列.
(1)求证:数列{an}是等差数列;
(2)若bn=an f (an),且数列{bn}的前n项和为Sn,当m=3时,求Sn;
(3)若cn= f(an) lg f (an),问是否存在m,使得数列{cn}中每一项恒不小于它后面的项?若存在,求出m的取值范围;若不存在,请说明理由.