已知函数f(x)是定义在R上的奇函数,并且当x∈(0,+∞)时,f(x)=2x.
(1)求f(log2 )的值;
)的值;
(2)求f(x)的解析式.
(本小题满分为14分)已知定义域为R的函数 是奇函数.
是奇函数.
(1)求a,b的值;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
设定义域为 的单调函数
的单调函数 ,对任意
,对任意 ,都有
,都有 ,若
,若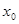 是方程
是方程 的一个解,且
的一个解,且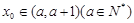 ,则实数
,则实数 =.
=.
(本小题满分14分)已知函数
 .
.
(1)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)若对于任意 都有
都有 成立,求实数
成立,求实数 的取值范围;
的取值范围;
(3)若过点 可作函数
可作函数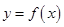 图象的三条不同切线,求实数
图象的三条不同切线,求实数 的取值范围.
的取值范围.
(本小题满分14分)设椭圆
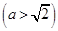 的右焦点为
的右焦点为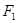 ,直线
,直线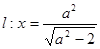 与
与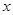 轴交于点
轴交于点 ,若
,若 (其中
(其中 为坐标原点).
为坐标原点).
(1)求椭圆 的方程;
的方程;
(2)设 是椭圆
是椭圆 上的任意一点,
上的任意一点,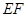 为圆
为圆 的任意一条直径(
的任意一条直径( 、
、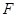 为直径的两个端点),求
为直径的两个端点),求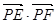 的最大值.
的最大值.
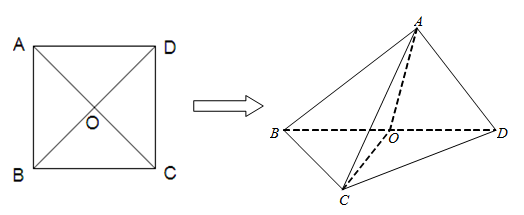
(本小题满分14分)如图所示,已知正方形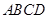 的边长为2,
的边长为2, .将正方形
.将正方形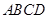 沿对角线
沿对角线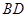 折起,得到三棱锥
折起,得到三棱锥 .
.
(1)求证:平面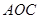
 平面
平面 ;
;
(2)若三棱锥 的体积为
的体积为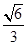 ,求
,求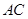 的长.
的长.