据气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).
(1)当t=4时,求s的值;
(2)将s随t变化的规律用数学关系式表示出来;
(3)若N城位于M地正南方向,且距M地650 km,试判断这场沙尘暴是否会侵袭到N城,如果会,在沙尘暴发生后多长时间它将侵袭到N城?如果不会,请说明理由.
已知椭圆 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线 相切.
相切.
(1)求椭圆C的方程;
(2)设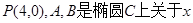 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结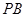 交椭圆
交椭圆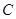 于另一点
于另一点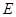 ,证明:直线
,证明:直线 与x轴相交于定点
与x轴相交于定点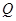 ;
;
(3)在(2)的条件下,过点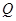 的直线与椭圆
的直线与椭圆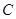 交于
交于 、
、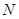 两点,求
两点,求 的取值范围.
的取值范围.
设数列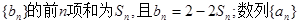 为等差数列,且a5=14,a7=20。
为等差数列,且a5=14,a7=20。
(I)求数列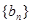 的通项公式;
的通项公式;
(II)若
某市近郊有一块500m×500m的正方形的荒地,地方政府准备在此块荒地中建一个综合性休闲广场,休闲广场为图所示的一个矩形场地,其总面积为3000平方米,其中阴影部分为通道,通道宽度均为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为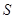 平方米.
平方米.
(1)分别写出用 表示
表示 和
和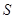 的函数关系式(写出函数定义域);
的函数关系式(写出函数定义域);
(2)怎样设计(当 和
和 分别取何值时)才能使
分别取何值时)才能使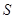 取得最大值,最大值为多少?
取得最大值,最大值为多少?
如图,在底面为直角梯形的四棱锥
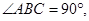
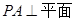
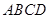 ,
,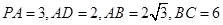 ,
,
(1)求证: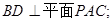
(2)求二面角 的大小.
的大小.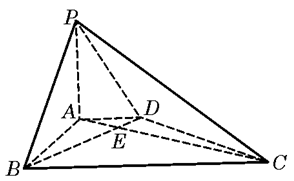
已知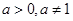 ,命题
,命题 函数
函数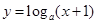 在
在 上单调递减,命题
上单调递减,命题 曲线
曲线 与
与 轴交于不同的两点,若
轴交于不同的两点,若 为假命题,
为假命题,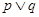 为真命题,求实数
为真命题,求实数 的取值范围.
的取值范围.