如图,在△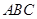 中,
中,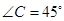 ,
, 为
为 中点,
中点, .记锐角
.记锐角 .且满足
.且满足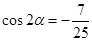 .
.
(1)求 ;
;
(2)求 边上高的值.
边上高的值.
(本小题满分12分)如图,在直三棱柱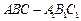 中,
中, ,
, ,
,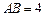 ,
,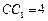 ,E在
,E在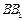 上,且
上,且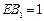 ,
,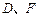 分别为
分别为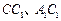 的中点.
的中点.
(1)求证: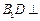 平面
平面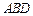 ;
;
(2)求异面直线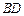 与
与 所成的角;
所成的角;
(3)求点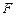 到平面
到平面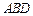 的距离.
的距离.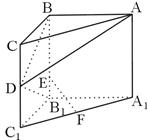
(本小题满分12分)要建造一个容积为2000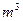 ,深为5
,深为5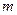 的长方体无盖蓄水池,池壁的造价为95
的长方体无盖蓄水池,池壁的造价为95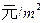 ,池底的造价为135
,池底的造价为135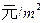 ,若水池底的一边长为
,若水池底的一边长为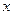
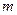 ,水池的总造价为
,水池的总造价为 元。(1)把水池总造价
元。(1)把水池总造价
 表示为
表示为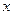 的函数。(2)当水池
的函数。(2)当水池 的长
的长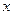 为多少时,水池的总造价最少?
为多少时,水池的总造价最少?
(本小题满分12分)在△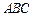 中,角
中,角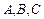 所对边分别为
所对边分别为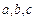 ,且
,且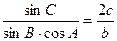 .(1)求角A;(2)若
.(1)求角A;(2)若
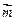
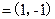 ,
,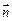 =
=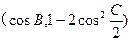 ,,试求
,,试求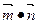 的取值范围.
的取值范围.
(1)如图,向量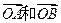 被矩阵M作用后分别变成
被矩阵M作用后分别变成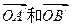 ,
,
(Ⅰ)求矩阵M;(Ⅱ)并求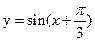 在M作用后的函数解析式;
在M作用后的函数解析式;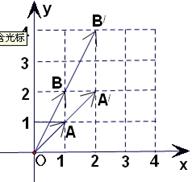
(2)已知在直角坐标系x0y内,直线l的参数方程为 .以Ox为极轴建立极坐标系,曲线C的极坐标方程为
.以Ox为极轴建立极坐标系,曲线C的极坐标方程为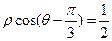 .若C与L的交点为P,求点P与点A(-2,0)的距离|PA|。
.若C与L的交点为P,求点P与点A(-2,0)的距离|PA|。
已知函数 .
.
(Ⅰ)求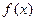 的极值;
的极值;
(II)判断y=f(x)的图像是否是中心对称图形,若是求出对称中心并证明,否则说明理由;
(III)设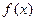 的定义域为
的定义域为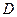 ,是否存在
,是否存在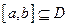 .当
.当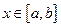 时,
时,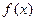 的取值范围是
的取值范围是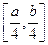 ?若存在,求实数
?若存在,求实数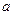 、
、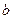 的值;若不存在,说明理由
的值;若不存在,说明理由