已知函数 .
.
(Ⅰ)求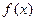 的极值;
的极值;
(II)判断y=f(x)的图像是否是中心对称图形,若是求出对称中心并证明,否则说明理由;
(III)设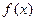 的定义域为
的定义域为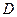 ,是否存在
,是否存在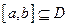 .当
.当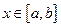 时,
时,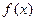 的取值范围是
的取值范围是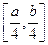 ?若存在,求实数
?若存在,求实数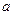 、
、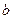 的值;若不存在,说明理由
的值;若不存在,说明理由
(本小题满分12分)为迎接2015年在兰州举行的“中国兰州国际马拉松赛”,某单位在推介晚会中进行嘉宾现场抽奖活动.抽奖盒中装有大小相同的 个小球,分别印有“兰州马拉松”和“绿色金城行”两种标志,摇匀后,规定参加者每次从盒中同时抽取两个小球(登记后放回并摇匀),若抽到的两个小球都印有“兰州马拉松”即可中奖,并停止抽奖,否则继续,但每位嘉宾最多抽取
个小球,分别印有“兰州马拉松”和“绿色金城行”两种标志,摇匀后,规定参加者每次从盒中同时抽取两个小球(登记后放回并摇匀),若抽到的两个小球都印有“兰州马拉松”即可中奖,并停止抽奖,否则继续,但每位嘉宾最多抽取 次.已知从盒中抽取两个小球不都是“绿色金城行”标志的概率为
次.已知从盒中抽取两个小球不都是“绿色金城行”标志的概率为 .
.
(1)求盒中印有“兰州马拉松”标志的小球个数;
(2)用 表示某位嘉宾抽奖的次数,求
表示某位嘉宾抽奖的次数,求 的分布列和期望.
的分布列和期望.
(本小题满分12分)如图,在四棱柱 中,底面
中,底面 是等腰梯形,
是等腰梯形, ∥
∥ ,
, ,
, ,顶点
,顶点 在底面
在底面 内的射影恰为点
内的射影恰为点 .
.
(1)求证: ;
;
(2)若直线 与直线
与直线 所成的角为
所成的角为 ,求平面
,求平面 与平面
与平面 所成角(锐角)的
所成角(锐角)的
余弦函数值.
(本小题满分12分)在 中,角
中,角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,已知
,已知 .
.
(1)求 的大小;
的大小;
(2)若 ,求
,求 的取值范围.
的取值范围.
(本小题满分l0分)选修4—5:不等式选讲
已知函数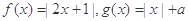
(1)当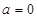 时,解不等式
时,解不等式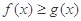 ;
;
(2)若存在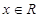 ,使得,
,使得,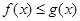 成立,求实数
成立,求实数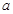 的取值范围.
的取值范围.
(本小题满分10分)选修4—4:坐标系与参数方程
在直角坐标系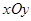 中,圆
中,圆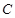 的参数方程
的参数方程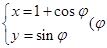 为参数).以
为参数).以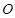 为极点,
为极点,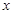 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求圆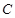 的极坐标方程;
的极坐标方程;
(2)直线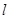 的极坐标方程是
的极坐标方程是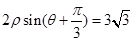 ,射线
,射线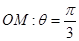 与圆
与圆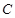 的交点为
的交点为 ,与直线
,与直线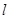 的交点为
的交点为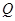 ,求线段
,求线段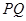 的长.
的长.