如图，在平面直角坐标系中，点O为坐标原点，以点A（0，-3）为圆心，5为半径作圆A，交x轴于B、C两点，交y轴于点D、E两点．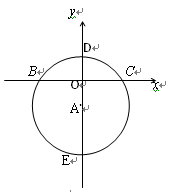
（1）如果一个二次函数图象经过B、C、D三点，求这个二次函数的解析式；
（2）设点P的坐标为（m，0）(m>5),
过点P作
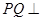x轴交（1）中的抛物线于点Q，当以
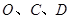为顶点的三角形与
相似时，求点P的坐标．
某校组织了“安全在我心中”知识竞赛活动.根据获奖同学在竞赛中的成绩制成的统计图表如下：
根据以上图表提供的信息，解答下列问题：
（1）写出表中x, y的数值；
（2）请补全频数分布直方图；
（3）如果成绩在95分以上（含95分）的可以获得特等奖，那么获奖的同学获得特等奖的概率是多少？
（4）获奖成绩的中位数落在哪个分数段？
如图，我国的一艘海监船在钓鱼岛A附近沿正东方向航行，船在B点时测得钓鱼岛A在船的北偏东60°方向，船以50海里/时的速度继续航行2小时后到达C点，此时钓鱼岛A在船的北偏东30°方向．请问船继续航行多少海里与钓鱼岛A的距离最近？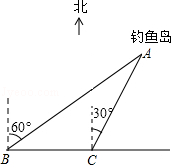
△ABC在平面直角坐标系xOy中的位置如所示．
（1）作△ABC关于点C成中心对称的△A1B1C1．
（2）将△A1B1C1向右平移3个单位，作出平移后的△A2B2C2．
（3）在x轴上求作一点P，使PA1+PC2的值最小，并写出点P的坐标（不写解答过程，直接写出结果）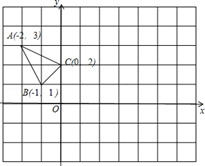
先化简，再求代数式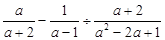
的值，其中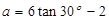
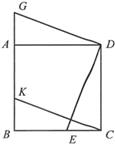
如图，四边形ABCD是正方形，点E，K分别在BC，AB上，点G在BA的延长线上，且CE=BK=AG．
（1）求证：①DE=DG； ②DE⊥DG
（2）尺规作图：以线段DE，DG为边作出正方形DEFG（要求：只保留作图痕迹，不写作法和证明）；
（3）连接（2）中的KF，猜想并写出四边形CEFK是怎样的特殊四边形，并证明你的猜想：
（4）当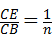
时，请直接写出
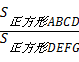的值．