如图,已知反比例函数 的图像经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB 的面积为2.若直线 y="ax+b" 经过点A,并且经过反比例函数
的图像经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB 的面积为2.若直线 y="ax+b" 经过点A,并且经过反比例函数 的图象上另一点C(n,一2).
的图象上另一点C(n,一2).
(1)求反比例函数 与直线y=ax+b的解析式;
与直线y=ax+b的解析式;
(2)根据所给条件,直接写出不等式 ax+b≥ 的解集_________________;
的解集_________________;
(3)求出线段OA的长,并思考:在x轴上是否存在一点P,使得△PAO是等腰三角形,如果存在,请求出P的坐标,如果不存在,请说明理由。
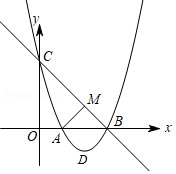
已知抛物线 过点 , 两点,与 轴交于点 , .
(1)求抛物线的解析式及顶点 的坐标;
(2)过点 作 ,垂足为 ,求证:四边形 为正方形;
(3)点 为抛物线在直线 下方图形上的一动点,当 面积最大时,求点 的坐标;
(4)若点 为线段 上的一动点,问: 是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由.
为了响应市政府号召,某校开展了“六城同创与我同行”活动周,活动周设置了“ :文明礼仪, :生态环境, :交通安全, :卫生保洁”四个主题,每个学生选一个主题参与.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下条形统计图和扇形统计图.

(1)本次随机调查的学生人数是 人;
(2)请你补全条形统计图;
(3)在扇形统计图中,“ ”所在扇形的圆心角等于 度;
(4)小明和小华各自随机参加其中的一个主题活动,请用画树状图或列表的方式求他们恰好选中同一个主题活动的概率.
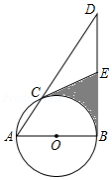
如图, 为 的直径,且 ,点 是 上的一动点(不与 , 重合),过点 作 的切线交 的延长线于点 ,点 是 的中点,连接 .
(1)求证: 是 的切线;
(2)当 时,求阴影部分面积.
天门山索道是世界最长的高山客运索道,位于张家界天门山景区.在一次检修维护中,检修人员从索道 处开始,沿 路线对索道进行检修维护.如图:已知 米, 米, 与水平线 的夹角是 , 与水平线 的夹角是 .求:本次检修中,检修人员上升的垂直高度 是多少米?(结果精确到1米,参考数据:

阅读下面的材料:
按照一定顺序排列着的一列数称为数列,数列中的每一个数叫做这个数列的项.排在第一位的数称为第一项,记为 ,排在第二位的数称为第二项,记为 ,依此类推,排在第 位的数称为第 项,记为 .所以,数列的一般形式可以写成: , , , , , .
一般地,如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,那么这个数列叫做等差数列,这个常数叫做等差数列的公差,公差通常用 表示.如:数列1,3,5,7, 为等差数列,其中 , ,公差为 .
根据以上材料,解答下列问题:
(1)等差数列5,10,15, 的公差 为 ,第5项是 .
(2)如果一个数列 , , , , ,是等差数列,且公差为 ,那么根据定义可得到: , , , , , .
所以
,
,
由此,请你填空完成等差数列的通项公式: .
(3) 是不是等差数列 , , 的项?如果是,是第几项?