已知数列 中,
中,  ,
,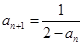 (
( ).
).
(1)计算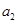 ,
, ,
,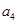 ;
;
(2)猜想数列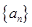 的通项公式并用数学归纳法证明.
的通项公式并用数学归纳法证明.
一盒中装有9张各写有一个数字的卡片,其中4张卡片上的数字是1,3张卡片上的数字是2,2张卡片上的数字是3,从盒中任取3张卡片.
(1)求所取3张卡片上的数字完全相同的概率;
(2)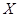 表示所取3张卡片上的数字的中位数,求
表示所取3张卡片上的数字的中位数,求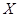 的分布列与数学期望.
的分布列与数学期望.
(注:若三个数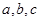 满足
满足 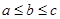 ,则称
,则称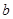 为这三个数的中位数).
为这三个数的中位数).
选修4-5:不等式选讲
设a,b,c均为正数,且a+b+c=1,证明:
(Ⅰ)ab+bc+ac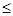
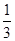 ;
;
(Ⅱ)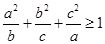 .
.
选修4-4:坐标系与参数方程
在直角坐标系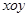 中,曲线
中,曲线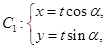 (
(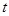 为参数,
为参数,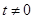 ),其中
),其中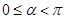 ,在以
,在以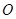 为极点,
为极点,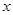 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线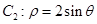 ,曲线
,曲线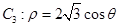 .
.
(Ⅰ).求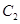 与
与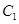 交点的直角坐标;
交点的直角坐标;
(Ⅱ).若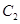 与
与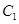 相交于点
相交于点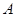 ,
,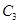 与
与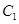 相交于点
相交于点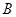 ,求
,求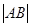 的最大值.
的最大值.
选修4-1:几何证明选讲
如图,P是 O外一点,PA是切线,A为切点,割线PBC与
O外一点,PA是切线,A为切点,割线PBC与 O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交
O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交 O于点E.
O于点E.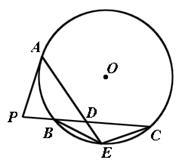
证明:(1)BE=EC;
(2)AD DE=2
DE=2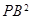 .
.
已知函数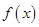 =
=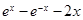 .
.
(1)讨论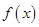 的单调性;
的单调性;
(2)设 ,当
,当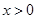 时,
时,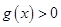 ,求
,求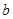 的最大值;
的最大值;
(3)已知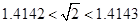 ,估计ln2的近似值(精确到0.001)
,估计ln2的近似值(精确到0.001)