已知椭圆 的左右焦点为
的左右焦点为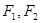 ,抛物线C:
,抛物线C: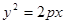 以F2为焦点且与椭圆相交于点
以F2为焦点且与椭圆相交于点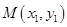 、
、
 ,点
,点 在
在 轴上方,直线
轴上方,直线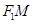 与抛物线
与抛物线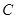 相切.
相切.
(1)求抛物线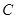 的方程和点
的方程和点 、
、 的坐标;
的坐标;
(2)设A,B是抛物线C上两动点,如果直线 ,
,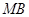 与
与 轴分别交于点
轴分别交于点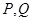 .
.  是以
是以 ,
, 为腰的等腰三角形,探究直线AB的斜率是否为定值?若是求出这个定值,若不是说明理由.
为腰的等腰三角形,探究直线AB的斜率是否为定值?若是求出这个定值,若不是说明理由.
.数列 的各项均为正数,
的各项均为正数,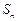 为其前
为其前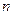 项和,对于任意
项和,对于任意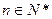 ,总有
,总有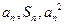 成等差数列.(Ⅰ)求数列
成等差数列.(Ⅰ)求数列 的通项公式;(Ⅱ)设数列
的通项公式;(Ⅱ)设数列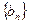 的前
的前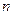 项和为
项和为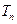 ,且
,且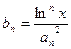 ,求证:对任意实数
,求证:对任意实数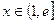 (
(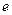 是常数,
是常数,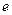 =2.71828
=2.71828 )和任意正整数
)和任意正整数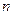 ,总有
,总有
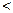 2;(Ⅲ) 正数数列
2;(Ⅲ) 正数数列 中,
中,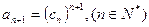 .求数列
.求数列 中的最大项.
中的最大项.
(本小题满分13分)已知点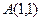 是椭圆
是椭圆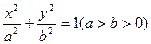 上的一点,
上的一点,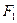 ,
,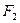 是椭圆的两个焦点,且满足
是椭圆的两个焦点,且满足 .(Ⅰ)求椭圆的方程及离心率;(Ⅱ)设点
.(Ⅰ)求椭圆的方程及离心率;(Ⅱ)设点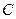 ,
,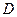 是椭圆上的两点,直线
是椭圆上的两点,直线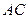 ,
,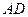 的倾斜角互补,试判断直线
的倾斜角互补,试判断直线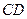 的斜率是否为定值?并说明理由.
的斜率是否为定值?并说明理由.
设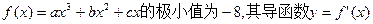
的图像经过点 如图所示,(Ⅰ)求
如图所示,(Ⅰ)求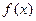 的解析式;
的解析式;
(Ⅱ)若对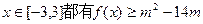 恒成立,
恒成立,
求实数m的取值范围.
(本题满分12分,第Ⅰ小题4分,第Ⅱ小题5分,第Ⅲ小题3分)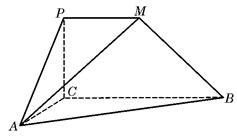 如图,
如图,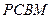 是直角梯形,∠
是直角梯形,∠ =90°,
=90°, ∥
∥ ,
, =1,
=1, =2,又
=2,又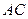 =1,∠
=1,∠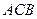 =120°,
=120°,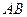 ⊥
⊥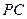 ,直线
,直线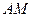 与直线
与直线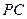 所成的角为60°.
所成的角为60°.
(Ⅰ)求证:平面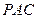 ⊥平面
⊥平面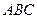 ;
;
(Ⅱ)求二面角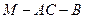 的大小;
的大小;
(Ⅲ)求三棱锥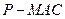 的体积.
的体积.
(本题满分12分)有人预测:在2010年的广州亚运会上,排球赛决赛将在中国队与日本队之间展开,据以往统计, 中国队在每局比赛中胜日本队的概率为 ,比赛采取五局三胜制,即谁先胜三局谁就获胜,并停止比赛.(Ⅰ)求中国队以3:1获胜的概率;(Ⅱ)设
,比赛采取五局三胜制,即谁先胜三局谁就获胜,并停止比赛.(Ⅰ)求中国队以3:1获胜的概率;(Ⅱ)设 表示比赛的局数,求
表示比赛的局数,求 的期望值.
的期望值.